Robust Classification with Convolutional Prototype Learning
一文是自动化所刘成林、殷飞老师组 Hong-Ming Yang 师兄的工作,CVPR 2018
录用。 论文地址:https://arxiv.org/abs/1805.03438v1
论文代码:https://github.com/YangHM/Convolutional-Prototype-Learning
这篇文章在原型学习(prototype learning)与 CNN
的基础之上,提出了一种有效的学习方式,并设计了几种不同的 loss
函数,这些损失函数均能从直观上理解其效果并在实验中证明它们的有效性。通过学习这篇文章,可以更好地了解原型学习以及
loss 的设计,同时可以直接将文中的方法用于一些下游应用。
此外需要注意的是,这篇文章的“Robust
classification”和 Goodfellow 提出的对抗样本型“Robust
model”是两码事。这篇文章没有对模型对于对抗样本的 Robust
进行分析,但本文提出的方法学习到的分类器对于任务来说是 Robust
的。从文章的实验结果来看,将这篇文章提出的方法称为“Robust”一点也不为过,毕竟“Robust”又不是
Goodfellow 发明的,各人可以有自己的理解。
概述
这篇文章主要按以下的框架描述了作者提出的方法:
- 背景与相关工作
- 卷积原型学习(Convolutional prototype learning)
- 设计的各种 loss 函数
- 实验结果与分析
因此,这篇笔记也按照论文作者的写作顺序记录。
背景与相关工作
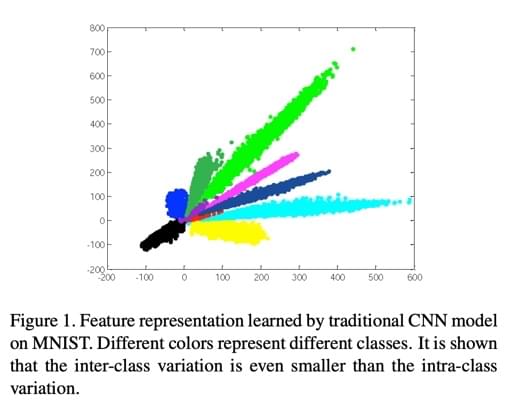
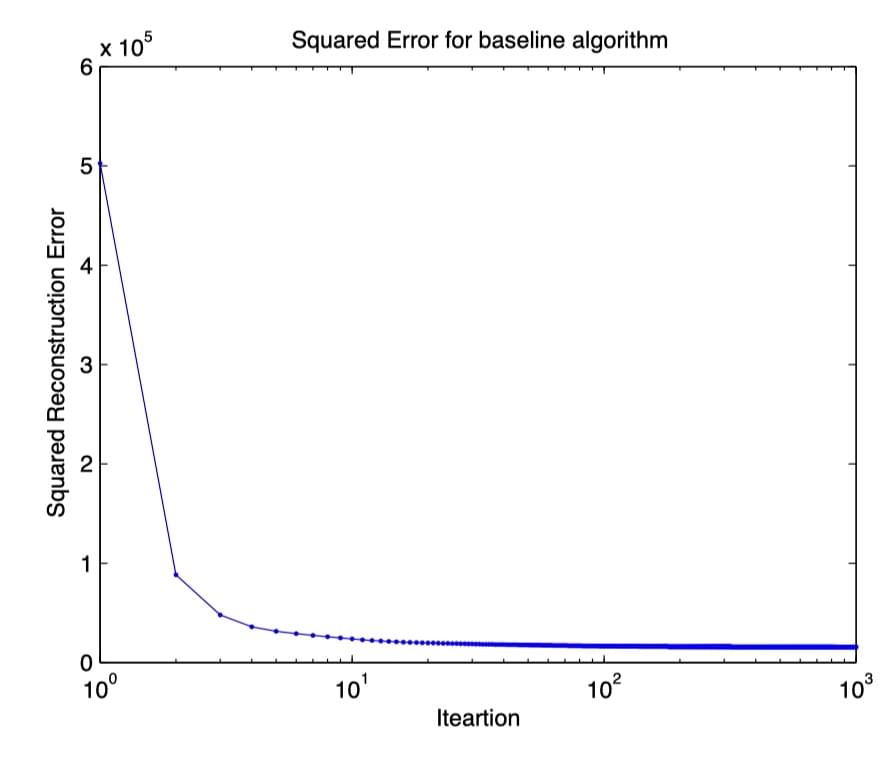
文章开头就给了这张图,描述了传统的 CNN 模型 + cross entropy loss 在
MNIST 上训练出来的特征的二维表示。作者用此图片说明了传统 CNN
模型的问题:学习出来的分类特征在特征空间内非常集中,甚至有很多类内距离(intra-class)小于类间距离(inter-class)的情况。这种情况也就会导致最终的分类效果变差,并且分类模型不易拓展等不够“Robust”的问题。
这个图片的具体作图方法,是把模型输出层前的最后隐层(bottleneck
layer)设定为两个神经元,训练完成后,将样本送入神经网络,取出这两个神经元的输出,将输出分别设为
X 与 Y
轴,即得到了这张图。(这个方法可以用在别的需要可视化特征的场景中,可以免去
PCA 等降维步骤。不过在一些比较复杂的任务里貌似这么训练会很难收敛)
尽管后来还有人为此做了各种改进,比如 triple loss、centre loss
等,来改善这种情况,但这些方法都没有离开 softmax + cross entropy
的范畴,也没有根本解决问题。因此作者基于原型学习的思想,利用 CNN
作为特征提取的工具,提出了一种原型学习框架 Convolutional prototype
learning(后文直接记为 CPL),同时为它设计了几种模式的 loss
函数,在实验上取得了良好的效果。
关于什么是原型学习,可以了解一下 LVQ 算法。
卷积原型学习
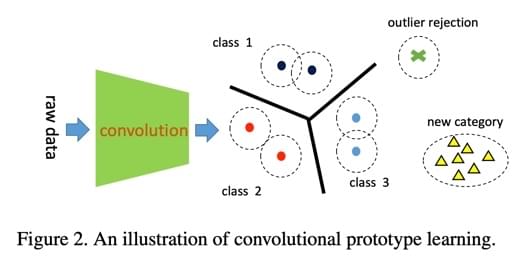
如图所示。这个框架其实思路很简单:
- 利用 CNN 进行特征提取:直接将 CNN 看做是一个 \(f(x,\theta)\) 的函数,输入的 x
是数据,\(\theta\) 是 CNN
的参数;输出的是特征。
- 用一个或多个原型来对应每一个分类(文章后来用实验证明了一个分类对应一个原型就可以有足够好的效果)。
- 在训练时,让原型与原型间的欧式距离尽量远,让特征与对应类别原型的欧式距离尽量近:
\[ \begin{array} { l } { x \in \text {
class arg } \max _ { i = 1 } ^ { C } g _ { i } ( x ) } \\ { g _ { i } (
x ) = - \min _ { j = 1 } \left\| f ( x ; \theta ) - m _ { i j } \right\|
_ { 2 } ^ { 2 } } \end{array} \]
(上式中各符号代表的含义请参考原论文 3.1 与 3.2)
loss 函数
这部分是文章的核心。为了实现上面一节说的 CPL,必须要有合适的 loss
函数,这种 loss 函数需要满足以下几个条件:
- 符合 CPL
的思路,及让原型与原型间距离尽量远,让特征与对应原型的距离尽量近。
- 需要对 CNN 可导(这样才能通过 BP 算法去优化 CNN 的参数 \(\theta\),也就才能让 CNN
提取出正确的特征)
- 需要对原型可导(这样才符合原型学习的思想,才能去不断调整原型在特征空间中的位置)
因此,这篇文章设计的几个 loss 函数都会去证明 \(\frac { \partial l } { \partial f }\) 与
\(\frac { \partial l } { \partial M }\)
的可导性。(l 是 loss 函数,f 是 CNN 特征提取器,M
是原型集),笔记中就不再赘述。
下文将逐个说明论文提出的 loss 函数。
Minimum classification
error loss(MCE)
MCE 即“最小分类误差”,是《Discriminative learning for minimum error
classification》提出的一种经典的测量指标,主要公式如下:
\[\mu _ { y } ( x ) = - g _ { y } ( x ) +
\left[ \frac { 1 } { C - 1 } \sum _ { j \neq y } g _ { j } ( x ) ^ {
\eta } \right] ^ { 1 / \eta }\]
作者在列这个公式的时候貌似忘了解释 \(\eta\)
的作用了。查阅原文发现,这个指标可以用来控制考虑误分类的程度多少。当
\(\eta\) 为正无穷的时候,上式等于
\[\mu _ { y } ( x ) = - g _ { y } ( x ) +
g _ { r } ( x )\]
其中 \(g _ { r } ( x ) = \max _ { k \neq y
} g _ { k } ( x )\),是“错的最离谱”的错分距离。因此可以将 MCE
记为
\[\mu _ { y } ( x ) = \left\| f ( x ) - m
_ { y i } \right\| _ { 2 } ^ { 2 } - \left\| f ( x ) - m _ { r j }
\right\| _ { 2 } ^ { 2 }\]
作者按照《Discriminative learning for minimum error
classification》中的 Translated sigmoid 公式定义了这个方法最终的 loss
函数计算公式:
\[l ( ( x , y ) ; \theta , M ) = \frac { 1
} { 1 + e ^ { - \xi \mu _ { y } } }\]
综上,这个 loss 方法其实优化的是 MCE 指标,重点是作者将 \(\mu_y\)
转换为了原型的形式,换句话就是说这个 loss 在优化时,除了会让 CNN
提取出正确的特征外,还会尽量让原型靠近正确的类的特征分布密集区域,远离错误的类的特征分布区域。通过这种方式,可以实现笔记最开头提到的目标。
Margin based classification
loss(MCL)
顾名思义,这个 loss 是“基于边距的分类 loss”。这个“margin”在 triple
loss
等方法中其实都有用到。作者提出这个方法的思想就是“让一个样本的特征和对应分类的原型在特征空间中的距离,要小于和其它原型在特征空间内的距离”,通过这种思路,就能使得样本尽量不被误分类。按照这个思路,作者提出了公式:
\[l ( ( x , y ) ; \theta , M ) = \left[ d
\left( f ( x ) , m _ { y i } \right) - d \left( f ( x ) , m _ { r j }
\right) \right] _ { + }\]
这个公式中的 d 函数就是求样本和原型在特征空间中的欧式距离。整个 loss
用 \(\left[ \right] _+\)
包含着,表示只取正值。因为如果样本距离正确分类的原型的距离已经满足要求时,loss
值应该为 0。
根据上式,作者进一步对这个 loss 进行完善,为它添加了 margin(作用和
triple loss、centre loss 的 margin
是一致的),让“样本离本类原型”的距离要比“样本离其它类原型”距离+margin要更小:
\[l ( ( x , y ) ; \theta , M ) = \left[ d
\left( f ( x ) , m _ { y i } \right) - d \left( f ( x ) , m _ { r j }
\right) + m \right] _ { + }\]
这样就能达成前文所说的目的。
作者在此基础上,又为 margin 的值做了进一步的改进。因为在上述 loss
中,margin
的值必须和“样本与原型的距离”值在同一个数量级上才能顺利进行优化。为此,作者稍作转换:
\[l ( ( x , y ) ; \theta , M ) = \left[
\frac { d \left( f ( x ) , m _ { y i } \right) - d \left( f ( x ) , m _
{ r j } \right) } { d \left( f ( x ) , m _ { y i } \right) + d \left( f
( x ) , m _ { r j } \right) } + m \right] _ { + }\]
这样,m 在 (0,1) 的范围内取值即可保证数量级的一致性。
Distance based cross
entropy loss(DCE)
这个 loss 函数是基于一个约等式:
\[p \left( x \in m _ { i j } | x \right)
\propto - \left\| f ( x ) - m _ { i j } \right\| _ { 2 } ^ { 2
}\]
这个式子的意义是,可以用“样本距离原型的距离”来测度“样本属于一个原型类别的概率”。这样就能用
cross entropy
之类的方法对概率进行优化了。因此,需要用一个确切的值来把上式给写出来,同时满足:
- 概率值是正数
- 所有概率(即一个样本属于各个原型的概率)的和需要为 1
为此,作者定义
\[p \left( x \in m _ { i j } | x \right) =
\frac { e ^ { - \gamma d \left( f ( x ) , m _ { i j } \right) } } { \sum
_ { k = 1 } ^ { C } \sum _ { l = 1 } ^ { K } e ^ { - \gamma d \left( f (
x ) , m _ { k l } \right) } }\]
此时,样本属于一个分类的概率即为样本属于这个分类的各个原型的概率之和,即为:
\[p ( y | x ) = \sum _ { j = 1 } ^ { K } p
\left( x \in m _ { y j } | x \right)\]
应用 cross entropy,可以将最终的 loss 函数写出来:
\[l ( ( x , y ) ; \theta , M ) = - \log p
( y | x )\]
这个 loss 相当于换了一个角度考虑,把距离换成了概率然后代入 cross
entropy。
Generalized CPL with
prototype loss(GCPL)
除了上述的 loss 之外,作者还提出了一种可以加入上述 loss
中的约束方法。作者给的理由是,由于 CPL 中的参数比较少(因为 CNN
的参数本来就不多),很容易过拟合,因此需要这么一个约束来防止 overfit
情况的发生:
\[p l ( ( x , y ) ; \theta , M ) = \left\|
f ( x ) - m _ { y j } \right\| _ { 2 } ^ { 2 }\]
这个式子的意义是,计算在特征空间内样本的位置与对应分类的原型(且为距离最近的一个原型)位置的距离。利用这个约束,可以将前文提到的几种
loss 记为:
\[\operatorname { loss } ( ( x , y ) ;
\theta , M ) = l ( ( x , y ) ; \theta , M ) + \lambda p l ( ( x , y ) ;
\theta , M )\]
上式中的 \(\lambda\)
作用是控制此约束的强硬程度。通过这个约束,可以让同类的原型间的距离更近,不同类的原型间的距离更远。与此同时,就能保证样本在特征空间中的类内距离更近,类间距离更远。
实验结果
基于以上方法,作者在 MNIST、CIFAR-10、OLHWDB
数据集上进行了实验。其中,OLHWDB
数据集是一个大规模的中文手写文字数据集,甚至比 ImageNet
还要大。(不过我觉得作者还是应该在 ImageNet
上进行实验,不然整个实验还是不够完整。另外,作者的实验虽然都很置信且完善,但是对比实验选择的
baseline 不够 solid,只用了最基本的 softmax
作为对比,没有考虑最近几年涌现出的各种 softmax 的进阶版。)
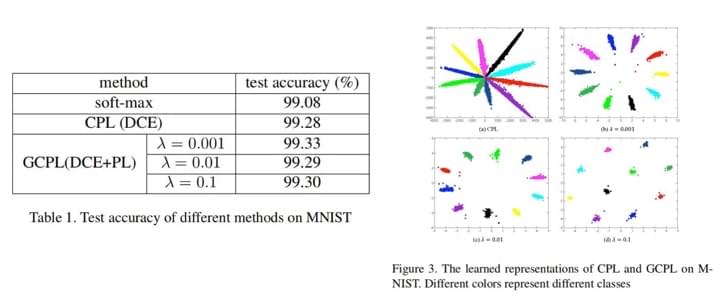
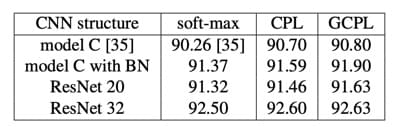
基本分类实验结果
可以看到,结果还是不错的,至少证明这篇文章提出的方法在最基本的分类效果上不会比
softmax 差。
拒识实验
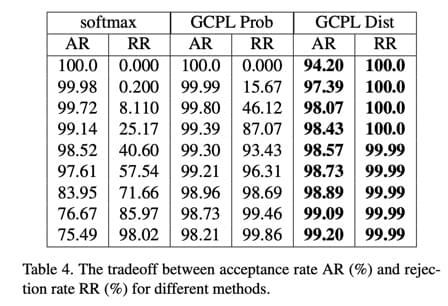
这个实验结果比较亮眼。最近对模型的“拒识能力”的要求越来越高,所谓拒识,就是在输入
invalid 的测试样本时,模型可以判断出这个是 out-of-domain
的东西,返回拒绝的结果。
作者的实验方法是,在 MNIST 上进行训练,然后混入 CIFAR
数据集的数据来测试模型的拒识能力。在这种 open-domain
的实验中,我们经常会用某种类似于 min-confidence
的指标来判断送入的数据是不是 out-of-domain,但是像传统的 softmax +
cross-entropy 方法中,min-confidence
越大,拒识率虽然会增加,但是准确率却也会明显下降。
作者提出的方法由于让不同类别的特征分布非常紧密,留出了大量的类间空间,因此在拒识率这块效果很好。
不过这个实验结果表格还是很微妙,因为每一横行参数啥的都不一样,虽然是为了做
AR 和 RR 的 trade-off 研究,但这样放着还是很奇怪。
类增量实验
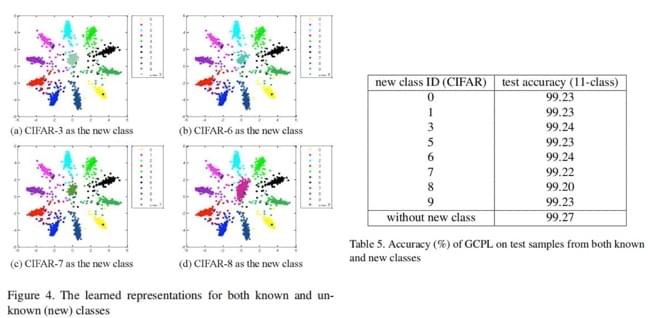
这个实验其实还不是很常见,一般在 life-long learning
相关的工作里会有这个实验。目的是,测试一个模型在训练完成后新增一个类别的能力。对于标准的
softmax + cross-entropy
来说,自然不存在这一种能力,原因可以参考这篇笔记的第一个图,本来各个类就离的近了,再加一个类直接就乱套了。
而本文的方法,可以在“基本分类实验”一章的图中看出,样本按照类原型聚集的非常紧密。这样新增一个类并不是什么很困难的事。
作者的实验方法是,在 MNIST 训练出的模型中,增加 CIFAR-10
的类。可以看上图,做出来的结果依然很不错。
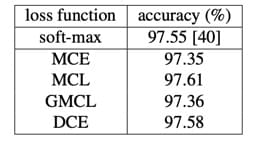
小样本训练
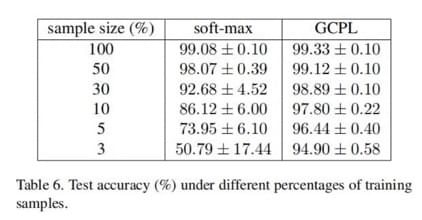
这个实验其实槽点也是 baseline 太 weak
了。现在做小样本的模型其实不占少数,但作者还是只选了 softmax
做比较。尽管如此,可以看到 GCPL 的效果还是很不错的。
多原型实验
前面的所有实验都是在“一个类别对应一个原型”的设定之下完成的,都有不错的效果。作者在文章最后用“一个类别对应多个原型”的假设进行了实验,结果如下表所示:

可以观察到,一个类别对应的原型数量其实对结果没有太大的影响。作者给出的解释是,CNN
提取特征的能力已经足够强大,即使初始数据的分布非常复杂,经过 CNN
变换之后,依然可以得到符合单高斯分布的特征分布,也就是一个类别一个原型的分布。
不过,在更复杂的情景下,一些更复杂的分类状况,多原型可能会发挥它应有的作用。
这块其实也是 trade-off。因为增加一个原型相当于在隐层输出时增加了
Dense Node,会极大地增加空间占用和计算量。
总结
这篇文章提出的方法足够新颖,并且取得的结果也非常好。虽然实验部分有些小遗憾(没有和各个任务顶尖的方法对比),但是仍然体现了这篇文章方法的综合性能的优越性。