本文作于 2018 年,被 AAAI 2019 接收。作者是浙大博士,在 Northwestern
University
做博后期间做出了此工作。文章中开源了实现代码:https://github.com/yao8839836/text_gcn
概述
本文解决的是自然语言处理中最基础的任务 -
文本分类任务。利用近年大火的图神经网络,作者通过词与文章的共现信息和
TF-IDF 权重和互信息权重将无结构数据文本进行了构图,并利用 Graph
Convolutional
Network(GCN)捕获图中的文档-词、词-词、文档-文档关系,从而进行文本分类。
具体来说,本文主要有以下两个贡献点:
提出了使用图神经网络来解决文本分类问题,有效利用了文档、词等的异构信息
在 benchmark 上达到了 state-of-the-art 的效果
背景与相关工作
文本分类
传统的文本分类方法主要依靠特征工程,在深度学习兴起后,各种深度学习框架代替了这个步骤。人们利用文本的分布式表示(embedding),使用各种
CNN、RNN、LSTM 等神经网络来捕获 embedding
中的语义信息,进行分类。本文就是在此基础之上,用 GCN 来捕获 Graph 中的
语义信息从而实现准确分类。
图网络
近些年为了突破传统神经网络只能应用于对齐的 grid
数据的限制,出现了可以应用于 Graph 的图神经网络。其中,GCN
方法简单有效,在图的各个节点上计算其邻居的聚合信息表示。因此,作者
employ 了 GCN 方法,将其用于图结构的学习。
数据
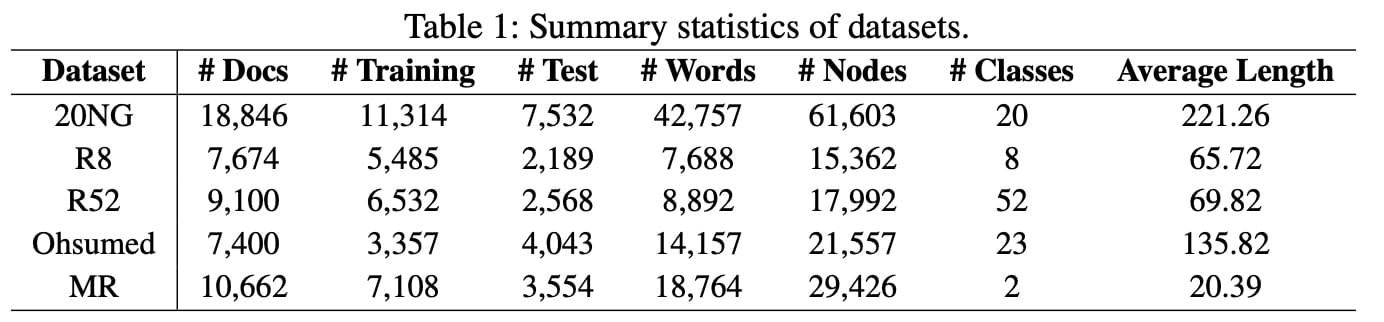
作者在 5 个常用的公开数据集上进行了实验。这 5
个数据集的基本信息如下:
-w692
在实验前,作者利用 NLTK 去除了前 4 个数据集的停用词,并去除了频次小于
5 的低频次。MR 数据集因为句子太短了,没有必要再删。
方法
构图方法
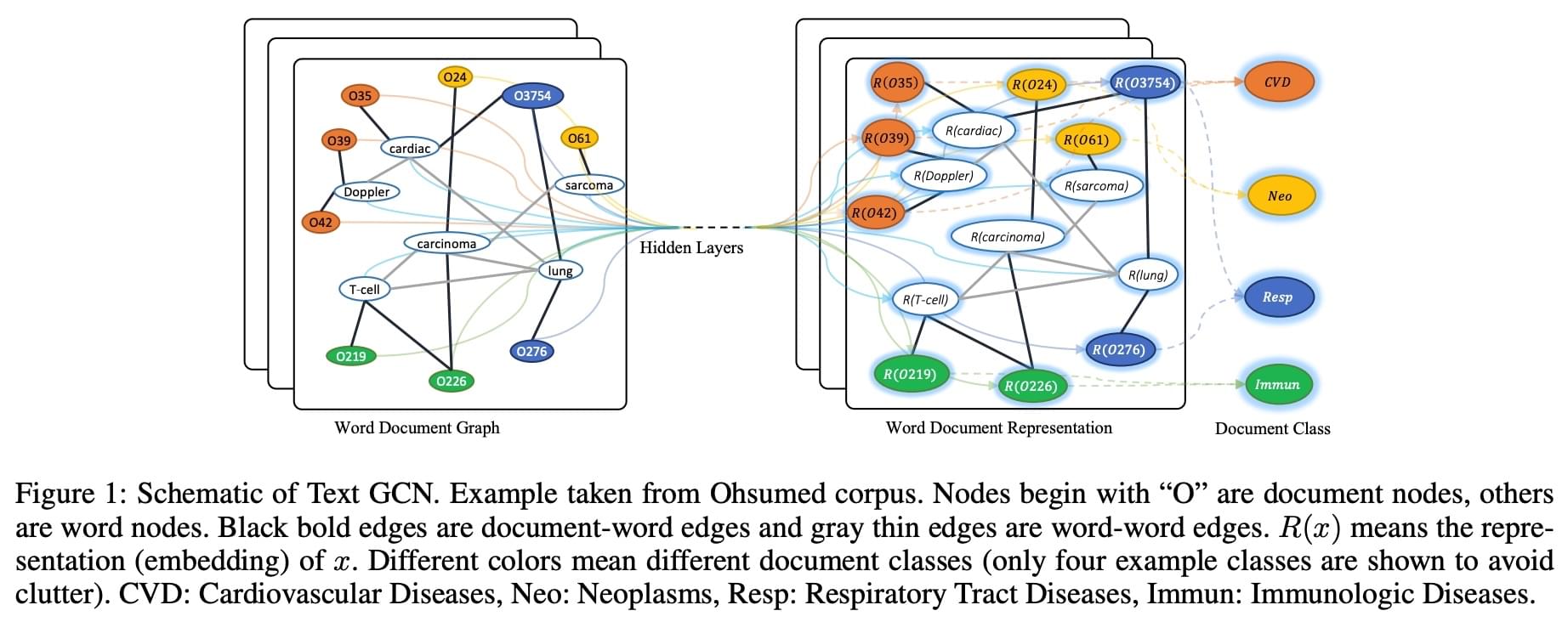
作者最终构成的图结构如下图所示:
-w922
在图中,左边是文本构成的图,右边是经过 GCN
得到的图表示。在左图中,以“O”开头的节点是文档节点,白色圈里有单词的节点是单词节点,黑色的线是文档-单词关系,灰色的线是单词-单词关系。右图中的\(R(x)\) 表示文档或单词\(x\) 的表示。
具体来说,在这个情景中,构图主要在于如何对文档-单词和单词-单词的边赋权。作者使用了下面公式所示的构图方式:
\[
A _ { i j } = \left\{ \begin{array} { c } { \operatorname { PMI } ( i ,
j ) } \space \text{i,j 是单词,且 PMI(i,j)>0} \\ { \mathrm { TF } -
\mathrm { IDF } _ { i j } } \space \text{i是单词,j是文档} \\ { 1 }
\space i =j \\ { 0 } \space otherwise \end{array} \right.
\]
\(A_{ij}\) 表示从节点 i 连到节点 j
的边的权重。简单来说,就是对文档-单词的边算 TF-IDF
作为权重,对单词-单词的边使用 PMI 做权重。PMI
是单词与单词的互信息,具体计算方式是:
\[
\begin{aligned} \operatorname { PMI } ( i , j ) = & \log \frac { p (
i , j ) } { p ( i ) p ( j ) } \\ p ( i , j ) = & \frac { \# W ( i ,
j ) } { \# W } \\ p ( i ) = & \frac { \# W ( i ) } { \# W }
\end{aligned}
\]
其中,#W 是滑动窗口,具体来说,PMI 就是算单词 i 和单词 j
同时出现的概率比上单词 i 和单词 j 单独出现的概率。
分类算法
在 GCN 框架内,使用 BP 算法来优化节点表示,并在 GCN 后加一层 Dense
层和激活层,利用 softmax 来进行分类。作者将其表示如下:
\[Z = \operatorname { softmax } \left(
\tilde { A } \operatorname { ReL } \mathbf { U } \left( \tilde { A } X W
_ { 0 } \right) W _ { 1 } \right)\]
其中,$ X W _ { 0 } $ 和前面的公式 \(L ^ {
( 1 ) } = \rho \left( \tilde { A } X W _ { 0 } \right)\)
一致,都是通过对 W
的优化来进行节点的表示。对上面的公式进一步拆解,可以记为:
\[E _ { 1 } = \tilde { A } X W _ { 0
}\]
\(E_1\)
就是对单词和文档节点的表示。
\[E _ { 2 } = \tilde { A } \operatorname {
ReLU } \left( \tilde { A } X W _ { 0 } \right) W _ { 1 }\]
\(E_2\)
就是对节点的第二层级表示。因此,本文相当于用了 2 层 GCN
进行图表示,然后用 softmax
进行分类。在分类优化时,采用了交叉熵损失函数:
\[
\mathcal { L } = - \sum _ { d \in \mathcal { Y } _ { D } } \sum _ { f =
1 } ^ { F } Y _ { d f } \ln Z _ { d f }
\]
实验
baseline 设置
作者设置了多种 baseline,包括:
TF-IDF + 线性分类器
CNN 文本分类(Convolutional neural networks for sentence
classification,EMNLP)
LSTM 文本分类(Recurrent neural network for text classification with
multi-task learning,IJCAI)
Bi-LSTM
PV-DBOW(Distributed representations of sentences and
documents,ICML)
PV-DM(同上)
PTE(Automatic lymphoma classification with sentence subgraph mining
from pathology reports)
FastText(Bag of tricks for efficient text classification,EACL)
SWEM(Baseline needs more love: On simple wordembedding-based models
and associated pooling mechanisms,ACL)
LEAM(Joint embedding of words and labels for text
classification,ACL)
Graph-CNN-C(Convolutional neural networks on graphs with fast
localized spectral filtering,NIPS)
Graph-CNN-S(Spectral networks and locally connected networks on
graphs,ICLR)
Graph-CNN-F(Deep convolutional networks on graphstructured
data)
可以看到,作者的实验非常完善且置信,应用了当时几乎全部的文本分类方法来进行对比。
实验设置
作者用了 200 维作为 embedding 维数,20 作为滑动窗口大小,学习率设为
0.02,Dorpout 设为 0.5,分别随机采样 10 % 数据作为验证集和测试集。
实验结果
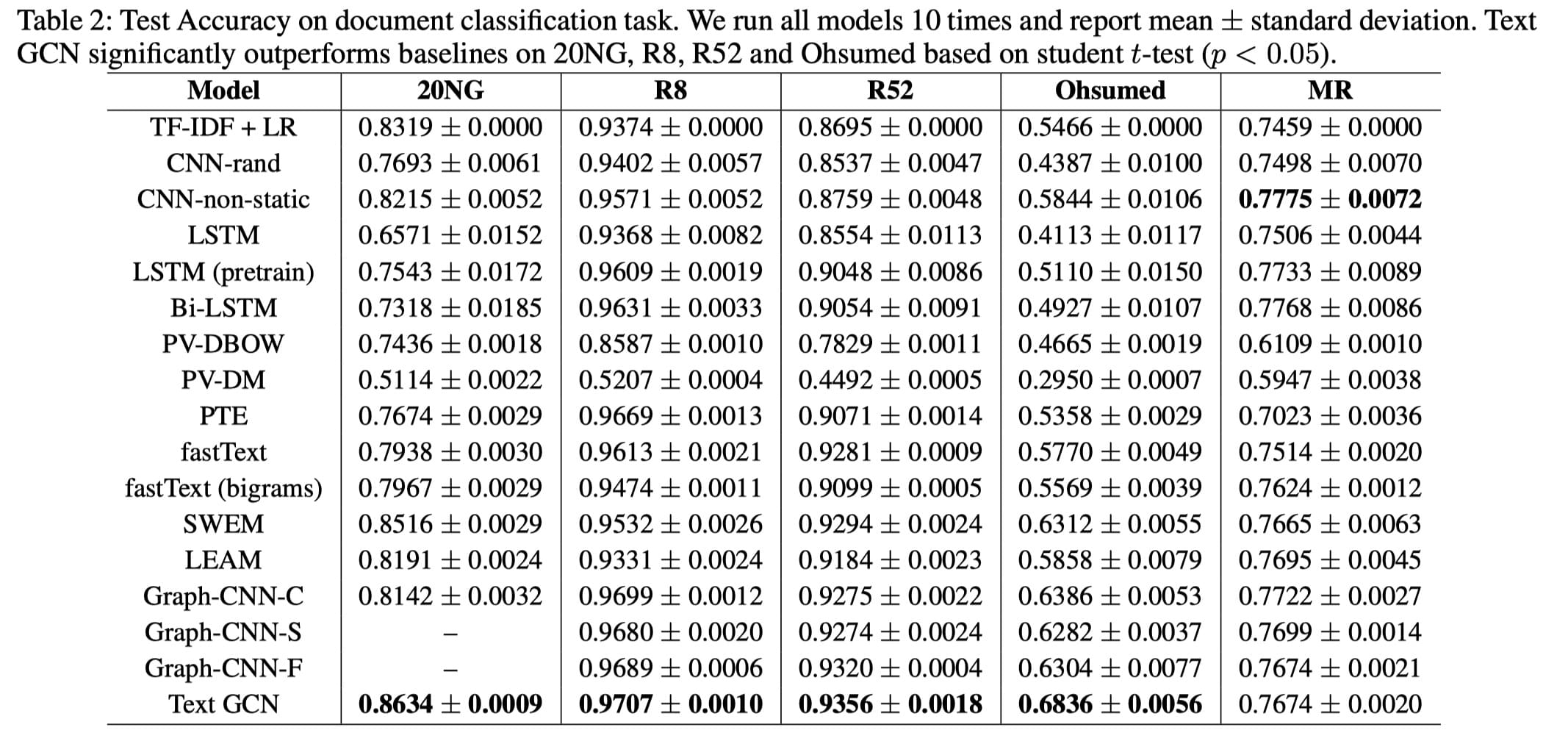
最终,得到了如下表所示的实验结果:
-w1067
该表有两个维度,数据集和模型。从此也可以看出,作者实验做的非常充分。
结果分析
从上表可以看到,除了 MR 数据集外,作者提出的 Text GCN
方法在其余全部数据集上都得到了最好的结果。猜测可能是由于 MR
数据集中数据过于短,构图效果不佳造成的。
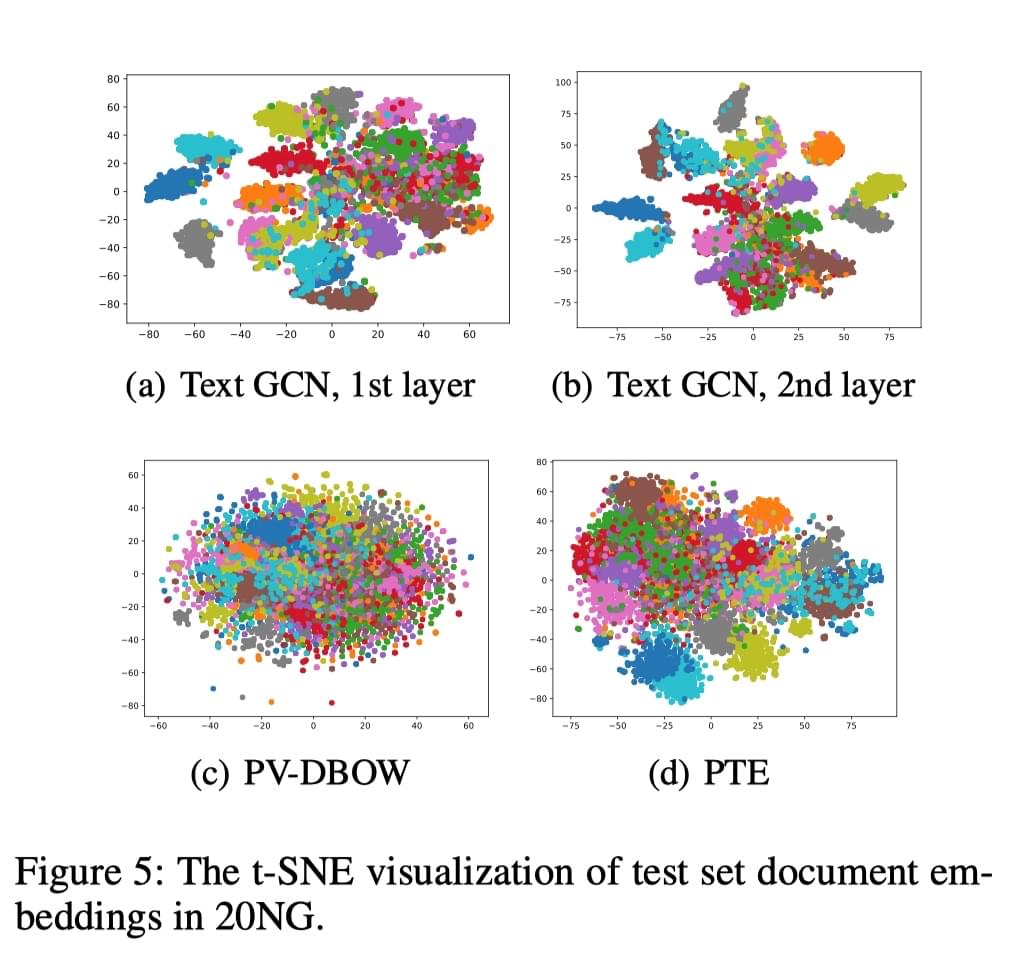
此外,作者利用 t-SNE 方法(Visualizing data using
t-sne,JMLR)对结果进行了可视化,用于分析训练得到的 embedding
的效果。结果如下:
-w513
可以看到,作者提出的 Text GCN 方法得到的文档表示在 t-SNE
表现是可分的,类间距离较大,优于用来对比的其余两种方法。
总结
作者提出的 Text GCN
方法在文本分类任务中,在多个数据集上得到了最好的结果。我认为其最大创新点在于:1、引入了
GCN 来做文本分类
2、提出了这种构建带权边图的方式。整个工作非常完备,应该要做的实验基本都做了,令人信服,我们做文本分类应当也要学习本文的实验方式。此外,文章最后的节点表示可视化也很有说服力。
对于后续工作,我觉得一个是可以 follow 一些新的构图方式和 GNN
框架,再有就是在 loss
方面进行改进,优化表示的空间分布。此外,可以考虑结合一些最新的语言模型方法(BERT、XLNET
等)改善结果。以及,可以对分类器那块进行一些改进,比如引入 Attention
等方法可能可以提升效果。