css控制文字自动换行并隐藏超出的部分
1 | display: -webkit-box; |
-webkit-line-clamp的数字代表文字最大为多少行。超出部分会用"..."代替
1 | display: -webkit-box; |
-webkit-line-clamp的数字代表文字最大为多少行。超出部分会用"..."代替
已经理解并明白了单变量线性回归与其对应的两个参数的梯度下降方程,现将情况推广到多元的情况。
例如最初的例子房价与房屋大小的关系,现在可以加上卧室数量、大厅数量、房屋年龄等其他的参数一并参与考虑来进行预测。
| Size(\(feet^2\)) | Number of bedrooms | Number of floors | Age of home(years) | Price($1000) |
|---|---|---|---|---|
| 2104 | 5 | 1 | 45 | 460 |
| 1416 | 3 | 2 | 40 | 232 |
| 1534 | 3 | 2 | 30 | 315 |
| 852 | 2 | 1 | 36 | 178 |
| ... | ... | ... | ... | ... |
在单变量线性回归中,样本的数量被记作m,在多元的情况下依然记为m,例如上表的数据有多少行m就为多少。
同时上表较之前多了几列,其特征数量即为n,即除了price之外的列数即为n,n=4。
同样将数据分为输入数据x与输出数据y,以m上标n下标的形式表现。例如上表的第三行表示的房子的层数就用\(x^{(3)}_3\)来表示。
因此由原来简单的
\[h_\theta(x)=\theta_0+\theta_1x\]
推广开来,成为了如下形式
\[h_\theta(x)=\theta_0+\theta_1x_1+\theta_2x_2+...+\theta_nx_n\]
为了定义方便,设x0=1,能得到对多元与单变量都适用的预测方程:
\[h(x)=\sum^n_{i=0}\theta_ix_i=\theta^TX\]
同样的,多元线性回归的预测方程也需要有值来评估预测拟合度的好坏,因此引入之前的代价方程,推广到多元情况,很容易得到代价方程(Cost Function):
\[J(\theta_0,\theta_1,...,\theta_n)=\frac{1}{2m}\sum^m_{i=1}(h_\theta(x^{(i)})-y^{(i)})^2\]
对于单变量线性回归来说,梯度下降的原理如下:

而对于多元线性回归来说,\(J(\theta_0,\theta_1)\)推广到了\(J(\theta_0,...,\theta_n)\),因此求偏导得到的结果有n种情况。
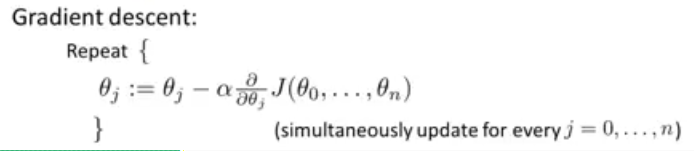
偏导得

\[ \theta_0:=\theta_0 - \alpha\frac{1}{m}\sum^m_{i=1}(h_\theta(x^{(i)})-y^{(i)})x^{(i)}_0\] \[ \theta_1:=\theta_1 - \alpha\frac{1}{m}\sum^m_{i=1}(h_\theta(x^{(i)})-y^{(i)})x^{(i)}_1\] \[ \theta_2:=\theta_2 - \alpha\frac{1}{m}\sum^m_{i=1}(h_\theta(x^{(i)})-y^{(i)})x^{(i)}_2\]
可以发现,最终得到的公式仍然符合单变量线性回归(n=1)。
偏导过程可由高数解出。
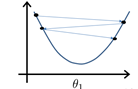
把一个参数的情形推广到两个参数,每个\(\theta_0\)都对应一组J与\(\theta_1\),表现在坐标图上呈现出一个碗状图形
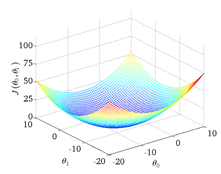 * * *
* * *
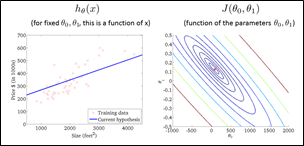
用了等高线的概念来理解这个图,可以做出它的“等高图”(轮廓图,contour figure)

横坐标与纵坐标便代表了两个参数,不同的圆弧代表了不同的代价函数值。
发现通过不断地降低J的值,可以得到更好的预测函数的拟合。
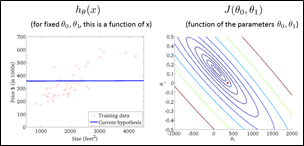
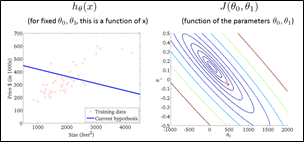
 * * *
* * *
为了让J尽可能的小,因此要同时考虑\(\theta_1\)与\(\theta_0\)的值。如果\(\theta_1\)保持不动,\(\theta_0\)就要往得到更小J的方向取值,反之亦然。可以理解成人站在山坡上,一步一步地向地势低的地方走,最终会到达“局部最低点”(local minimum)。
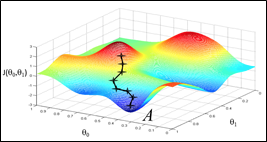
于是可以看到,影响这个过程的有几个因素:起始的位置,每步的步长和每个点的某方向上的斜率。
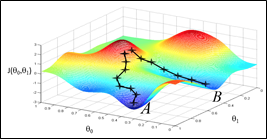
发现不同的起始位置可能会到达不同的局部最小值。因为这种“下山”的方式不是全面的,没有测算两个参数的所有情况。
回到只有一个参数的情况上看。
\(\theta_1:=\theta_1-\alpha\frac{d}{d\theta_1}J(\theta_1)\)( := 符号代表赋值)
\(\theta_1\)连续不断地减去当时的斜率与步长(合适的步长)的乘积,会向局部最小值滑动(可用高数证明),越接近局部最小值斜率就越小,值移动的就越慢,最后无限趋近到达导数为0的点。
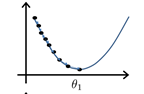
当步长的取值过大时,\(\theta_1\)有可能直接滑过局部最小值而到了极值点的另一侧,此时导数符号反转,与上面的趋近最小值的过程刚好相反,\(\theta_1\)越来越远离这个点。
但是当步长取值过小时,找到局部最小值的过程会变得太过漫长,效率低下 by the way,如果起始点一开始就在一个极小值点上时,其导数为0,它不再会发生变化
为了得到收敛值,可列出如下算式。

带入原式得
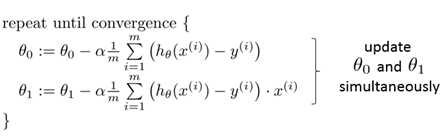
这就是梯度下降算法。
梯度下降算法能得到一个局部最优解,而对于线性回归问题来说,它的坐标图形是碗状的,只有一个最低点,因此用梯度下降法得到的点就是线性回归问题的全局最低值,使J最小,即全局最优解。
梯度下降算法一定是两个参数同时下降才能达到效果
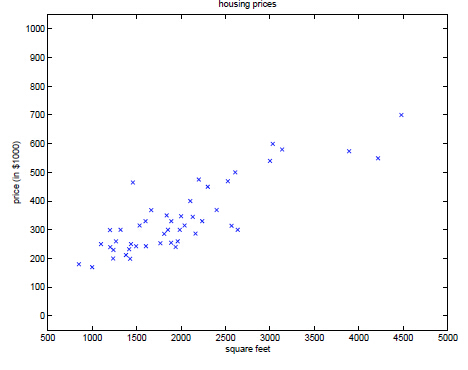
在监督学习中,有一种情况是数据集呈连续状分布,数据的几个值大致呈线性关系(如例子中的房价和房间大小的关系)。体现在坐标轴上如图下所示
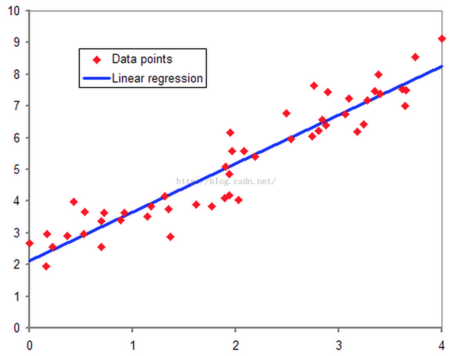
可以画出一条直线大概描述出整体数据的走向,这条直线被称为拟合曲线,在机器学习中直线代表的方程被称为预测(Hypothesis)方程,可以记作
\[ h_\theta(x)=\theta_0+\theta_1x \]
的形式,其中两个θ被称为预测方程的参数(Parameters),直接影响预测方程预测的准确性。
为了方便记录,整个数据集包含的样品数(坐标图上的所有点数)记作m,
每个点的x与y轴坐标一一对应,带入x值可以通过预测方程预测出y的大概值。因此称x为输入值(input),y为输出值(output)
为了表示预测方程预测的准确性,可以拿每个输入值x带入预测方程计算得到预测值h(x),再与实际值y进行比较。通过这种比较,能够衡量在这组参数下预估的结果和实际结果的差距,这样的计算方式称为代价函数(Cost Fuction)。比如说线性回归的代价函数定义为:
\[ J(\theta_0,\theta_1)=\frac{1}{2m}\sum^m_{i=1}(h_\theta(x^{(i)})-y^{(i)})^2 \]
(误差平方和函数是一个比较合适、常用的选择,当然,也可以选择一些其他形式的代价函数)
代价函数值越小,就说明当前参数值下的预测方程越准确。
为了得到尽量准确的预测方程,就要使J(代价函数)的值最小。现在单独将参数一个个拿出来看:
假设\(\theta_0=0\),即预测函数的直线经过原点。假定训练集为(1,1)(2,2)(3,3),很明显斜率为1的时候代价函数最小。
此时J=0,说明联系集的所有值全部符合预测方程。 > J=0时能说明预测方程符合程度较好,但不能说明接下来的数一定能够被完美预测。
当让\(\theta_1=0.5\)时,可以发现坐标图变成了如下所示
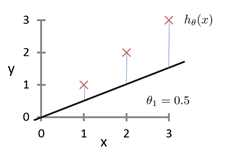
预测函数明显偏离了数据集。这时的代价函数值为
\[J(0)=\frac{1}{2 \times 3}[(0.5-1)^2+(1-2)^2+(1.5-3)^2]=\frac{3.5}{6}=0.58\]
当\(\theta_1=0\)时,
\[J(0)=\frac{1}{2 \times 3}[1^2+2^2+3^2]=\frac{14}{6}=2.3\]
可以发现偏差的越大,代价函数值越大。而且由于代价函数是平方差,因此参数往另一个方向变化也会有对称的变化。模型所预测的值与训练集中实际值之间的差距就是建模误差(modeling error)。
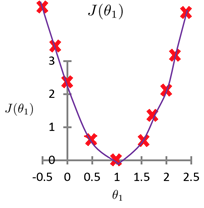
可以将代价函数值与参数\(\theta_1\)的值对应起来,坐标图如下
在项目中碰到了在v-for列表内还有一层列表的情况
json结构如下: 1
2
3
4
5
6
7
8
9
10
11
12{"orders":
[{"id":"1",
"state":"0",
"time":"2016-03-17",
"goods":[{"id":"1","name":"物品1","img":"xxx.jpg"},
{"id":"1","name":"物品1","img":"xxx.jpg"}]},
{"id":"2",
"state":"1",
"time":"2016-03-17",
"goods":[{"id":"1","name":"物品1","img":"xxx.jpg"},
{"id":"1","name":"物品1","img":"xxx.jpg"}]}
]}
可以看到需要在列表内嵌另一个列表。绑定代码为 1
2
3
4new Vue({
el: "#allorder",
data: order
})
html代码为 1
2
3
4
5
6
7
8
9<ul id="allorder" v-for="orders in orders">
<div class="order-state">{{orders.state}}</div>
订单号:<span>{{orders.id}}</span>
下单日期:<span>{{orders.ordertime}}</span>
<div class="lineimg" v-for="good in orders.goods">
<div class="item"><img v-bind:src="good.img_src"></div>
</div>
</div>
</ul>
the field of study that gives computers the ability to learn without being explicitly programmed
机器学习让计算机有能力去自主学习,而不是被死板地编程,它发源于人工智能领域,在现在各个领域发挥了独特的作用。
谷歌百度等搜索引擎实现的学习算法学会如何对网页排名,从而让海量的网页有序地展示在用户面前;
Iphone等手机与某些app在处理照片时,能够自动地识别出照片中的人;
电子邮箱系统在用户对广告邮件等标记垃圾邮件后,垃圾邮件过滤器学会了如何自动甄选出垃圾邮件,让用户避免垃圾邮件的困扰;
无人驾驶汽车通过图像或雷达等传感器学习大量正常驾驶时车辆的情景从而学会自己安全地驾驶;
在通过对各种棋谱、棋局的研究学习后,下棋软件能够打败世界一流的棋手;
等等...
机器学习的概念在很早之前就已经出现,例如神经元网络在1943年就已经被提出。 现在,网络技术与自动化技术飞速发展, 出现了大量的数据集可以运用与机器学习算法,例如网络企业的点击记录、医院的电子医疗记录、DNA测序等等;甚至机器学习算法已经被应用于探究人类的学习方式,并试图理解人类的大脑。
监督学习(Supervised learning)
无监督学习(Unsupervised learning)
强化学习(Reinforcement learning)等
包括回归问题(预测)、根据特征参数分类等。
举栗子:
(1)在收集大量关于某地房价与房屋面积的数据后,可以大致判断出房价与面积成线性关系,并能预测出数据中未包含的面积大小对应的大致的房价。
(2)在收集到大量某肿瘤病人的数据(如年龄与肿瘤大小)后,对病人的病情(如肿瘤良性恶性)进行输入,得到相关模型。之后的病人就可以根据其年龄、肿瘤大小直接预测出其所在分类(良性恶性)。
总结:在监督学习中,对于数据集中的每个数据, 都有相应的正确答案,(训练集) 算法就是基于这些来做出预测。例如上面的房价和肿瘤性质。
回归问题即预测一个连续值输出,分类问题即预测一个离散值输出。
无监督学习中没有监督学习数据集的属性、标签等,所有的数据都是一样的。
例如,
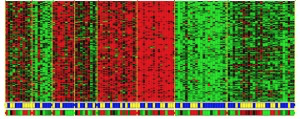
(1)聚类算法,在大量的没有明确标签的数据中,一些数据有着类似的特征或结构,通过聚类算法可以自动的找到这些数据中的类型。

例如DNA测序,测到的数值量非常大,不同DNA段可能有类似的功能与性质,通过聚类算法找到它们相似的性质并进
行分类。
(2)鸡尾酒宴问题:当两个人在同时说话时,有多个话筒分别在不同的位置对他们的声音进行采集,得到多个样本。经过算法处理后可以将两个人同时说话的声音分离开来(奇异值分解)。
对机器算法有了大概的认知与了解,对与监督学习与无监督学习的异同有了清楚的认识,能够正确地判断出某例是属于哪一类问题