机器学习学习笔记(二)
在监督学习中,有一种情况是数据集呈连续状分布,数据的几个值大致呈线性关系(如例子中的房价和房间大小的关系)。体现在坐标轴上如图下所示
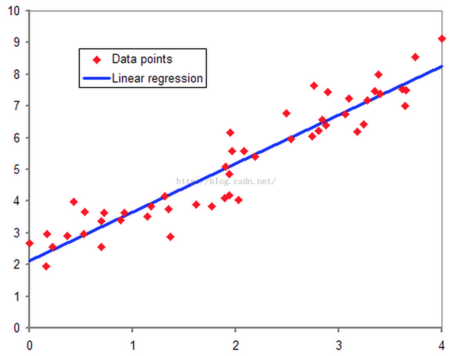
可以画出一条直线大概描述出整体数据的走向,这条直线被称为拟合曲线,在机器学习中直线代表的方程被称为预测(Hypothesis)方程,可以记作
\[ h_\theta(x)=\theta_0+\theta_1x \]
的形式,其中两个θ被称为预测方程的参数(Parameters),直接影响预测方程预测的准确性。
为了方便记录,整个数据集包含的样品数(坐标图上的所有点数)记作m,
每个点的x与y轴坐标一一对应,带入x值可以通过预测方程预测出y的大概值。因此称x为输入值(input),y为输出值(output)
为了表示预测方程预测的准确性,可以拿每个输入值x带入预测方程计算得到预测值h(x),再与实际值y进行比较。通过这种比较,能够衡量在这组参数下预估的结果和实际结果的差距,这样的计算方式称为代价函数(Cost Fuction)。比如说线性回归的代价函数定义为:
\[ J(\theta_0,\theta_1)=\frac{1}{2m}\sum^m_{i=1}(h_\theta(x^{(i)})-y^{(i)})^2 \]
(误差平方和函数是一个比较合适、常用的选择,当然,也可以选择一些其他形式的代价函数)
代价函数值越小,就说明当前参数值下的预测方程越准确。
为了得到尽量准确的预测方程,就要使J(代价函数)的值最小。现在单独将参数一个个拿出来看:
假设\(\theta_0=0\),即预测函数的直线经过原点。假定训练集为(1,1)(2,2)(3,3),很明显斜率为1的时候代价函数最小。
此时J=0,说明联系集的所有值全部符合预测方程。 > J=0时能说明预测方程符合程度较好,但不能说明接下来的数一定能够被完美预测。
当让\(\theta_1=0.5\)时,可以发现坐标图变成了如下所示
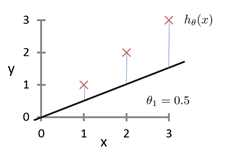
预测函数明显偏离了数据集。这时的代价函数值为
\[J(0)=\frac{1}{2 \times 3}[(0.5-1)^2+(1-2)^2+(1.5-3)^2]=\frac{3.5}{6}=0.58\]
当\(\theta_1=0\)时,
\[J(0)=\frac{1}{2 \times 3}[1^2+2^2+3^2]=\frac{14}{6}=2.3\]
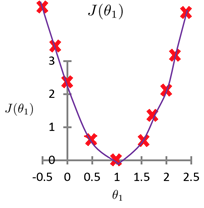
可以发现偏差的越大,代价函数值越大。而且由于代价函数是平方差,因此参数往另一个方向变化也会有对称的变化。模型所预测的值与训练集中实际值之间的差距就是建模误差(modeling error)。
可以将代价函数值与参数\(\theta_1\)的值对应起来,坐标图如下