An Online Social Network-based Recommendation System 论文笔记
本文发表于2007年,作者是来自多伦多大学计算机系的几位师生。虽然本文在领域内影响并不大,但我认为它的撰写非常清晰,有利于对“基于社会网络的推荐系统”这一课题的了解。
概述
作者提出了一种基于社会网络的推荐系统,这种推荐系统利用用户资料以及用户与用户之间的连接进行推荐(具体来说是通过用户的打分矩阵和对应的朋友关系来推荐)。 > 本文的数据来源于一个名为 BoardGameGeek(BGG)的网站,在数据一节详细描述
背景与相关工作
所谓推荐系统,是一种基于用户以往数据、通过某些算法计算,向用户推送新内容的一种机制,在 20 世纪互联网经济发展中被广泛使用。最早利用推荐系统扩大利润的是电商 Amazon,他们利用用户曾经购买或评分的商品来预测用户之后可能会购买的商品并进行推送,从而促使用户购买更多的商品。
推荐系统最常用的方式就是基于内容的协同过滤方法(这种方式在今天也被广泛使用,好处是推荐较为准确,坏处是计算量极大),具体来说就是通过计算多个用户喜好的相似,来推荐对应的对象。
推荐系统研究的一个难点就是数据的获取,使用用户数据容易触及隐私问题,因此各个公司都是在利用用户的公开数据来进行推荐系统的研究。这又有另一个问题:很多用户的公开数据并不完全(比如获取不到用户间的联系),导致困难重重。此外,传统的算法的前提假设为用户是独立的存在,因此无法利用用户的结构信息来进行推荐。
作者通过对社会学和机器学习的研究,为 boardgaming 开发了一种 Online Social Network-based(OSN)推荐系统,实现了较好的推荐效果。
最后作者还对数据的隐私问题和算法的应用进行了讨论。
数据
BoardGameGeek(BGG)是一个知名的游戏站点,人们在其中讨论各种游戏机和卡带,并且会对各个游戏、主机等产品进行评价、打分。比较特殊的是,这个网站包含了大量的公开社交信息(玩家会公开加好友,并进行讨论),因此适合用来使用社会网络来构建推荐系统。
最终,作者使用的数据包括:
- 大约 3 万条被用户评价过的游戏数据
- 大约 4 万条曾经评价过游戏的用户数据
- 所有的任意用户对任意游戏的评价数据
- 各个用户“愿望清单”的游戏列表
- 用户与用户之间的好友关系
算法
作者使用了概率矩阵分解算法(probabilistic matrix factorization,简称 PMF 算法)。在此简单描述一下这个算法:
给定一个维数为 \(M \times N\) 的评价矩阵 \(R\),其中 \(R_{ij}\) 可以表示用户 \(i\) 对游戏 \(j\) 的评价分数。而 PMF 算法的目的就是对评价矩阵 \(R\) 进行矩阵分解,找到评价矩阵的因子:
\[ R \approx U G\]
其中 $U ^ { M D } $, \(G \in \mathcal { R } ^ { D \times N }\)。作者假设有一些“原型用户”(prototype user),这种用户具有评分和喜好的代表性。上式中的\(D\)就是这种“原型用户”的数量。因此上面的矩阵分解就能得出原型用户的评分矩阵。作者直接利用 FA、PCA 之类的矩阵分解算法,使用方差 \(\left( \sum _ { i , j } R _ { i j } - U _ { i } ^ { T } G _ { j } \right) ^ { 2 }\) 作为损失函数,对矩阵分解算法进行优化。(注,这应该是非常稀疏的矩阵分析)
为了把社会网络的信息加入模型中,作者将社交信息定义为矩阵 \(F\),其维数是 \(M \times M\)。在 \(F\) 中,如果用户 \(i\) 和 \(j\) 是好友关系,则 \(F_{ij} = 1\),否则为 0。由此,作者将前面的矩阵分析式子改写为:
\[ R \approx F U G\]
转换问题,写作:
\[ F^{-1} R \approx U G\]
这样就可以继续用前文的方法求出原型用户的评分了。
实验
作者使用 SE(方差)loss 对矩阵分解进行优化,在训练迭代过程中 loss 下降情况如下图所示:
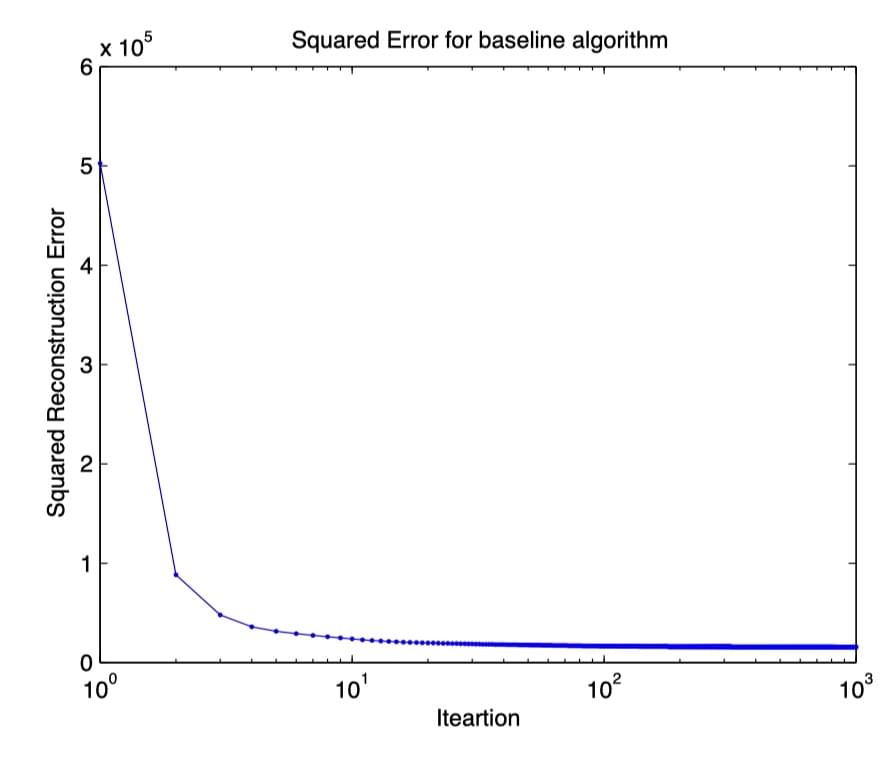
可以看到算法确实收敛了。(个人觉得可能过拟合了)
这个实验因为没有标注数据,所以也不好进行评价。因此作者用少数的数据作为测试集来验证效果,发现结果不错,最后直接将这个 baseline 做成了一款 Web 应用。
总结
本文提出了一种同时利用社会网络信息和用户评分信息的推荐算法,改善了推荐系统的效果。其意义是找了一种方法来把简单的社会网络信息给整合进传统的评分矩阵分解法中。总体来说整个文章的方法非常简单,而且实验不够置信,但可以用来参考了解“基于社会网络的推荐系统”这一课题。
此外,这篇文献的年代其实比较久远,目前已经有各种各样利用 Network Embedding 的方法,利用各种异构网络信息去做推荐系统,但其实主要的方法还是这篇文章中的方法:将评分矩阵与网络表示矩阵进行合并,然后再做矩阵分析。区别是本文的 Social Network 的表示实质上就是最简单的 one-hot Network Embedding,如果换成现代先进的 node2vec、deep walk 之类的方法应该会有所提升。