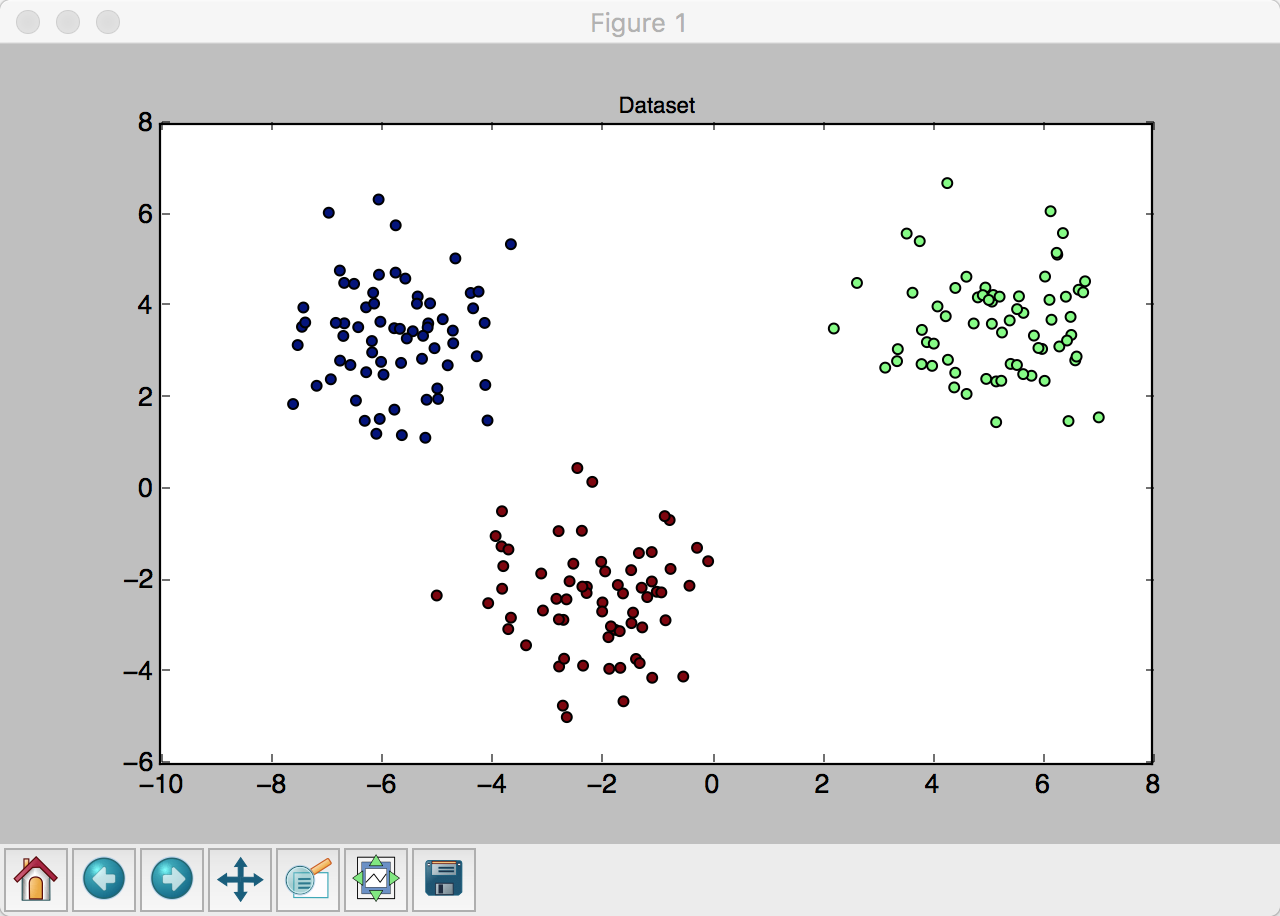
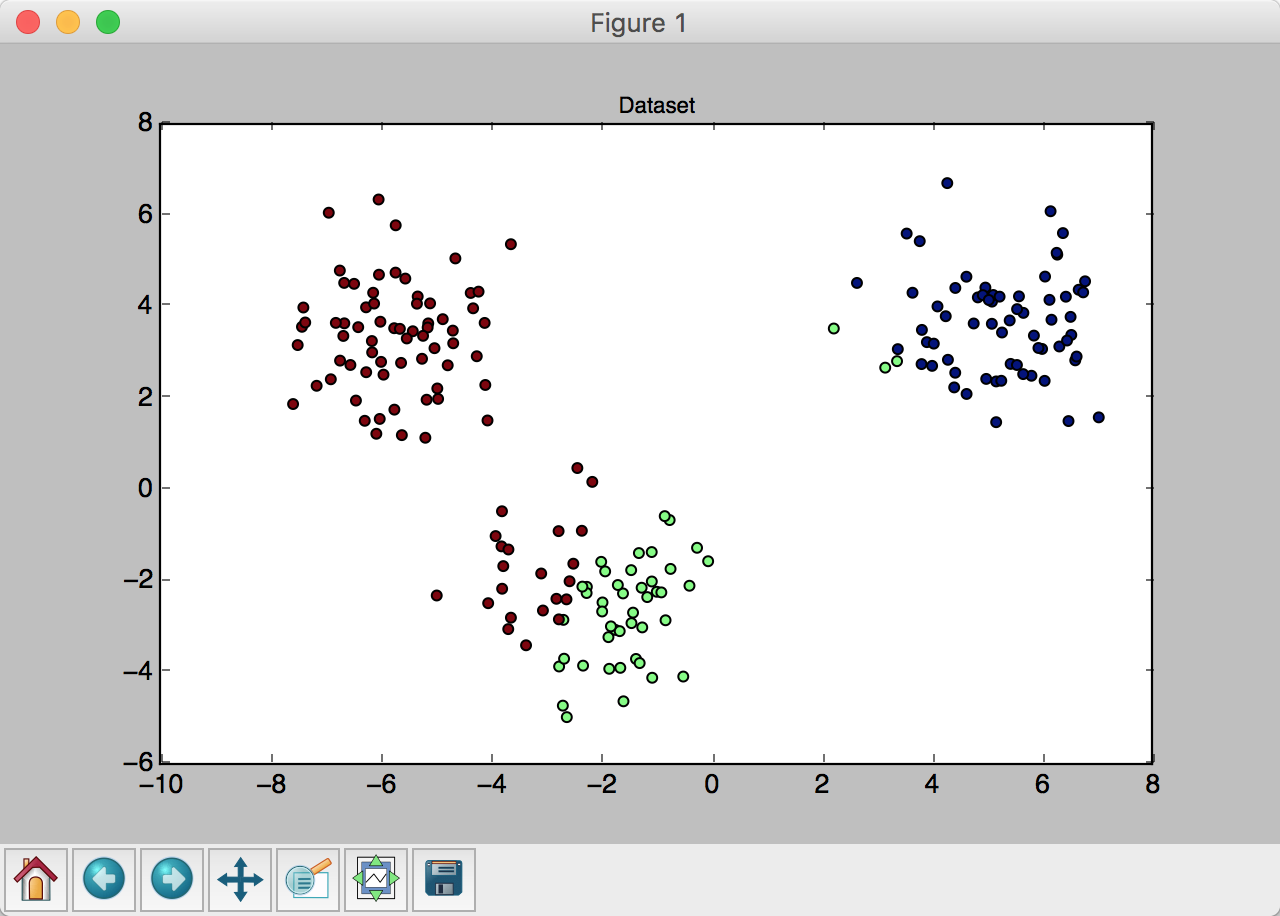
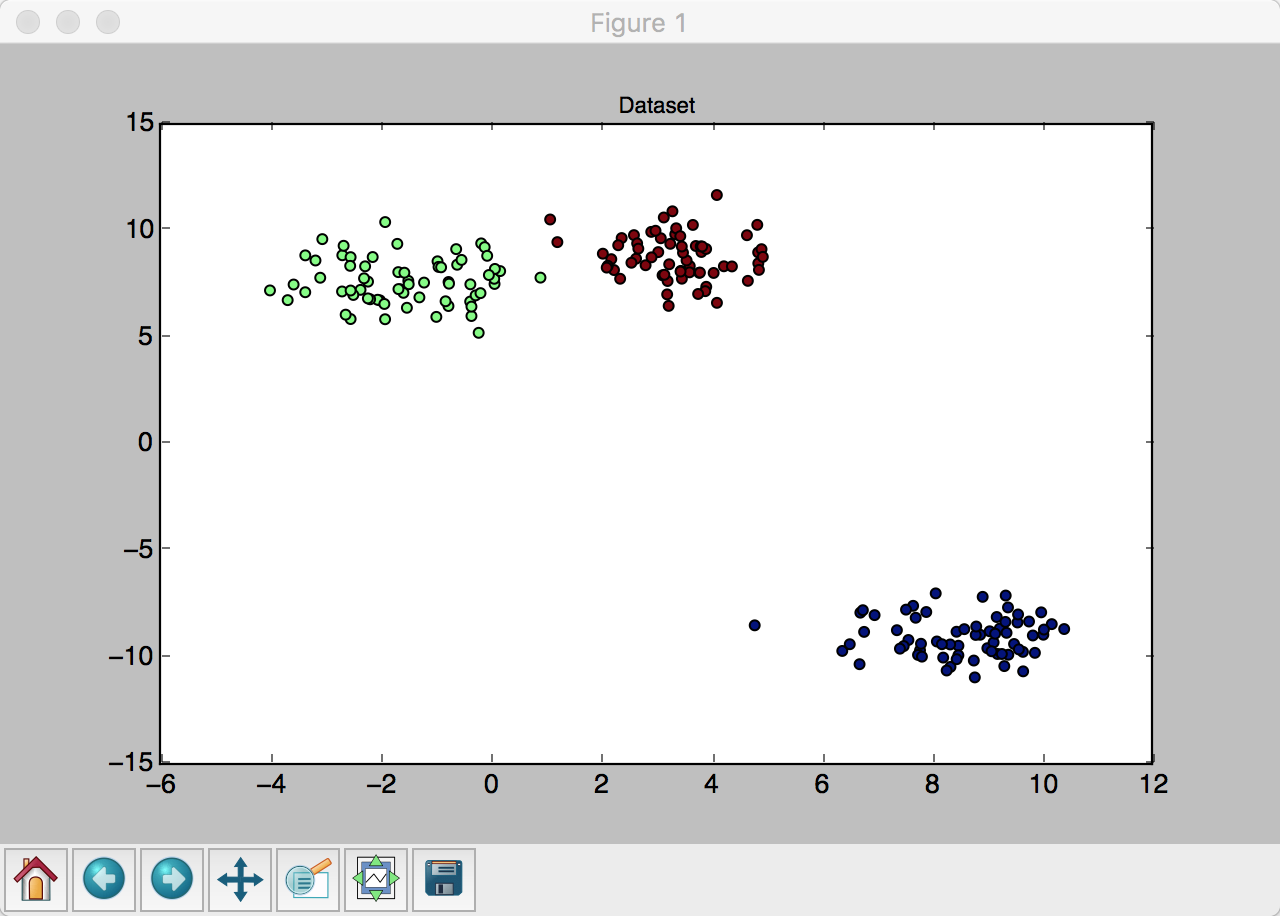
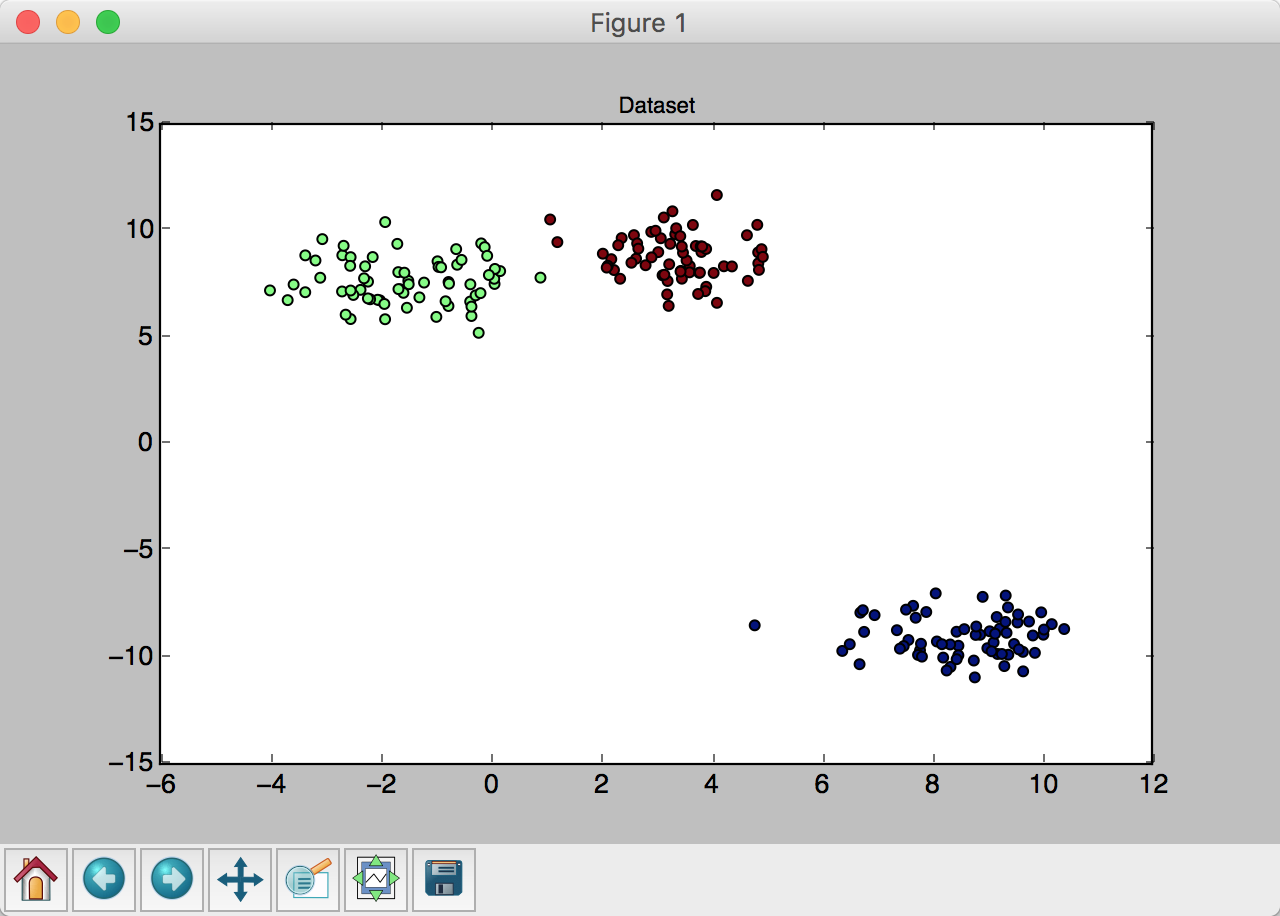
同中有异的 Webpack 与 Rollup

本周,Facebook 将一个非常大的 pull request 合并到了 React 主分支。这个 PR 将 React 当前使用的构建工具替换成了 Rollup。这让许多人感到不解,纷纷在推特上提问:“为什么你们选择 Rollup 而不选择 Webpack 呢?”1 2 3
有人问这个问题是很正常的。Webpack 是现在 JavaScript 社区中最伟大的成功传奇之一,它有着数百万/月的下载量,驱动了成千上万的网站与应用。它有着巨大的生态系统、众多的贡献者,并且它与一般的社区开源项目不同——它有着意义非凡的经济支持。
相比之下,Rollup 是那么的微不足道。但是,除了 React 之外,Vue、Ember、Preact、D3、Three.js、Moment 等众多知名项目都使用了 Rollup。为什么会这样呢?为什么这些项目不使用大家一致认可的 JavaScript 模块打包工具呢?
这两个打包工具的优缺点
Webpack 由 Tobias Koppers 在 2012 年创建,用于解决当时的工具不能处理的问题:构建复杂的单页应用(SPA)。尤其是它的两个特点改变了一切:
- 代码分割可以将你的 app 分割成许多个容易管理的分块,这些分块能够在用户使用你的 app 时按需加载。这意味着你的用户可以有更快的交互体验。因为访问那些没有使用代码分割的应用时,必须要等待整个应用都被下载并解析完成。当然,你也可以自己手动去进行代码分割,但是……总之,祝你好运。
- 静态资源的导入:图片、CSS 等静态资源可以直接导入到你的 app 中,就和其它的模块、节点一样能够进行依赖管理。因此,我们再也不用小心翼翼地将各个静态文件放在特定的文件夹中,然后再去用脚本给文件 URL 加上哈希串了。Webpack 已经帮你完成了这一切。
而 Rollup 的开发理念则不同:它利用 ES2015
模块的巧妙设计,尽可能高效地构建精简且易分发的 JavaScript
库。而其它的模块打包器(包括
Webpack在内)都是通过将模块分别封装进函数中,然将这些函数通过能在浏览器中实现的
require
方法打包,最后依次处理这些函数。在你需要实现按需加载的时候,这种做法非常的方便,但是这样做引入了很多无关代码,比较浪费资源。当你有很多模块要打包的时候,这种情况会变得更糟糕。
ES2015 模块则启用了一种不同的实现方法,Rollup 用的也就是这种方法。所有代码都将被放置在同一个地方,并且会在一起进行处理。因此得到的最终代码相较而言会更加的精简,运行起来自然也就更快。你可以点击这儿亲自试试 Rollup 交互式解释器(REPL)。
但这儿也存在一些需要权衡的点:代码分割是一个很棘手的问题,而 Rollup 并不能做到这一点。同样的,Rollup 也不支持模块热替换(HMR)。而且对于打算使用 Rollup 的人来说,还有一个最大的痛点:它通过插件处理大多数 CommonJS 文件的时候,一些代码将无法被翻译为 ES2015。而与之相反,你可以把这一切的事全部放心交给 Webpack 去处理。
那么我到底应该选用哪一个呢?
到目前为止,我们已经清晰地了解了这两个工具共存并且相互支撑的原因 — 它们应用于不同的场景。那么,现在这个问题的答案简单来说就是:
在开发应用时使用 Webpack,开发库时使用 Rollup
当然这不是什么严格的规定——有很多的网站和 app 一样是使用 Rollup 构建的,同时也有很多的库使用 Webpack。不过,这是个很值得参考的经验之谈。
如果你需要进行代码分割,或者你有很多的静态资源,再或者你做的东西深度依赖 CommonJS,毫无疑问 Webpack 是你的最佳选择。如果你的代码基于 ES2015 模块编写,并且你做的东西是准备给他人使用的,你或许可以考虑使用 Rollup。
对于包作者的建议:请使用
pkg.module!
在很长一段时间里,使用 JavaScript 库是一件有点风险的事,因为这意味着你必须和库的作者在模块系统上的意见保持一致。如果你使用 Browserify 而他更喜欢 AMD,你就不得不在 build 之前先强行将两者粘起来。通用模块定义(UMD)格式对这个问题进行了 部分 的修复,但是它没有强制要求在任何场景下都使用它,因此你无法预料你将会遇到什么坑。
ES2015 改变了这一切,因为 import 与 export
就是语言规范本身的一部分。在未来,不再会有现在这种模棱两可的情况,所有东西都将更加无缝地配合工作。不幸的是,由于大多数浏览器和
Node 还不支持 import 和
export,我们仍然需要依靠 UMD 规范(如果你只写 Node
的话也可以用 CommonJS)。
现在给你的库的 package.json 文件增加一个
"module": "dist/my-library.es.js"
入口,可以让你的库同时支持 UMD 与 ES2015。这很重要,因为 Webpack
和 Rollup 都使用了 pkg.module
来尽可能的生成效率更高的代码——在一些情况下,它们都能使用 tree-shake
来精简掉你的库中未使用的部分。
了解更多有关 pkg.module 的内容请访问 Rollup wiki
。
希望这篇文章能让你理清这两个开源项目之间的关系。如果你还有问题,可以在推特联系rich_harris、rollupjs、thelarkinn。祝你打包快乐!
感谢 Rich Harris 写了这篇文章。我们坚信开源协作是共同促进 web 技术前进的重要动力。
没有时间为开源项目做贡献?想要以其它方式回馈吗?欢迎通过 Open Collective 进行捐赠,成为 Webpack 的支持者或赞助商。Open Collective 不仅会资助核心团队,而且还会资助那些贡献出空闲时间帮助我们改进项目的贡献者们。
发布于掘金 https://juejin.im/post/58edb865570c350057f199a7