EM algorithm最大似然算法学习笔记
琴生不等式(Jensen's inequality)
最大似然函数应用到了琴生不等式。琴生不等式给出了积分的凸函数值和凸函数的积分值间的关系。它由以下两部分组成:
当\(f(x)\)是(a,b)区间上的凸函数时,则对任意的点\(x_1,x_2,...,x_n \in (a,b)\)有
\[f(\frac{x_1+x_2+...+x_n}{n}) \geq \frac{1}{n}[f(x_1)+f(x_2)+...+f(x_n)]\]
当\(x_1=x_2=...=x_n\)时取等号。
当\(f(x)\)是(a,b)区间上的凹函数时,则对任意的点\(x_1,x_2,...,x_n in (a,b)\)有
\[f(\frac{x_1+x_2+...+x_n}{n}) \leq \frac{1}{n}[f(x_1)+f(x_2)+...+f(x_n)]\]
当\(x_1=x_2=...=x_n\)时取等号。
将琴生不等式应用到概率论,有
当\(f(x)\)是凸函数时
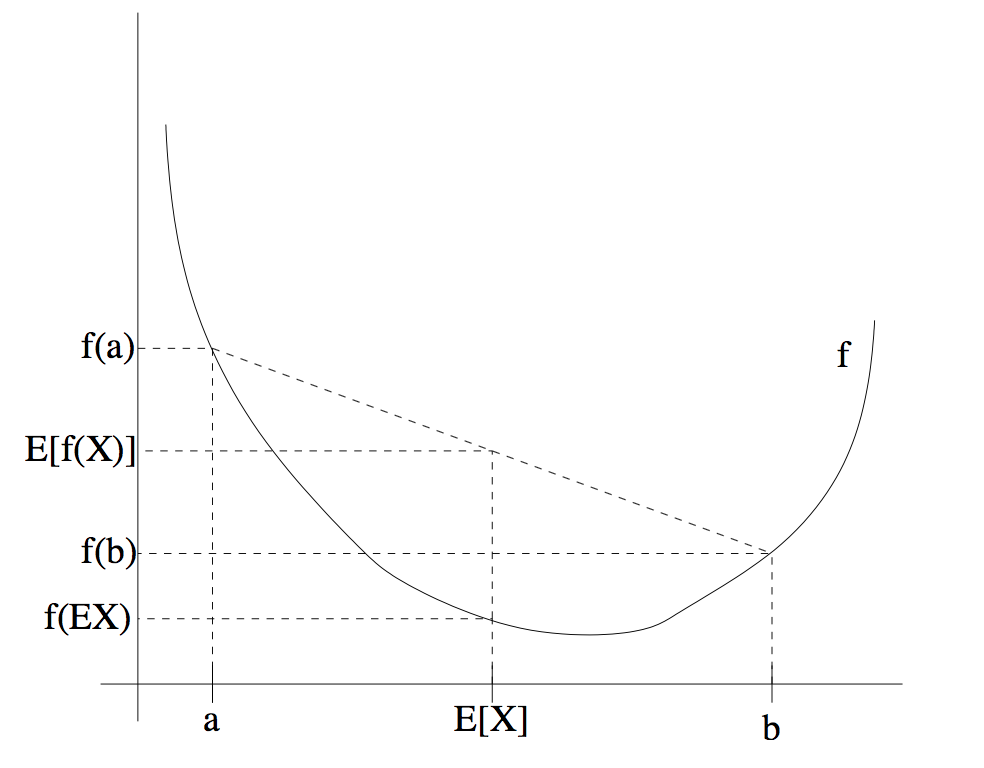
\[E[f(X)]\geq f(EX)\]
当\(f(x)\)是凹函数时
\[E[f(X)]\leq f(EX)\]
如图所示:
最大似然算法(EM algorithm)的推导
似然函数(likelihood function)
当有一组数据\({ x^{(1)},...,x^{(m)} }\),这一组数据是从更大的未知数据中抽样出来的,每一个x对抽样而言都是独立事件。因此,抽样出每个数据的概率为\(p(x)\),抽样出这一组数据集的概率则为\(\prod^m_{i=1} p(x)\)。而所有的数据都满足某一个分布规律(求的正是这个规律),例如高斯分布等。这个分布规律含有一个分布参数\(\theta\),这个参数决定了这个分布规律。此时抽样出数据集的概率为\(\prod^m_{i=1} p(x_i;\theta)\),将这个式子记为\(L(\theta)\),即
\[L(\theta)=\prod^m_{i=1} p(x_i;\theta)\]
当\(L(\theta)\)最大时,有最大的可能抽出这组数据,就能猜测\(\theta\)是分布概率的参数。这个式子被称为似然函数。
p(x;y)表示当参数为y时x的概率
为了让计算更方便,将乘法运算通过求ln值变化为加法运算
\[l(\theta)=\sum^m_{i=1} \ln p(x_i;\theta)\]
这个l称为loglikelihood function
最大似然函数
当有多组数据时,每组数据的分布规律都不同,对于每组数据来说都有一个隐藏的变量z将不同的组别分开。例如对于\(x^{(i)}\)来说,有\(p(z^{(1)})\)的可能是聚类1的,有\(p(z^{(2)})\)的可能是聚类2的。因此将所有的可能加起来,有
\[l(\theta)=\sum^m_{i=1} \ln p(x_i;\theta)=\sum^m_{i=1} ln\sum_{z^{(i)}}p(x^{(i)},z^{(i)};\theta)\]
为了求其最值,则需要对其进行求导。此时发现,\(\sum \ln \sum f(x,y,z)\)相当难进行求导,因此对其进行化简:
对于\(x^{(i)}\),它的所有z概率之和记为\(\sum_{z^{(i)}} Q_i(z^{(i)})=1\),对上式加入这个值,得到
\[l(\theta)=\sum^m_{i=1} \ln p(x_i;\theta)=\sum^m_{i=1} \ln\sum_{z^{(i)}} Q_i(z^{(i)}) \frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}\]
对于\(f(x)=\ln x\)来说,\(\frac{\mathrm{d}^2 f(x) }{\mathrm{d} x^2}=-\frac{1}{x^2}\leq0\),因此它为凹函数。应用琴生不等式,\(E(f(x)) \leq f(EX)\)。同理,上式进行不等变换:
\[f(E_{z^{(i)~Q_i}}[\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}]) \geq E_{z^{(i)~Q_i}}[f(\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})})]\Rightarrow \\ \sum^m_{i=1} ln\sum_{z^{(i)}} Q_i(z^{(i)}) \frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})} \\ \geq \sum^m_{i=1} \sum_{z^{(i)}} Q_i(z^{(i)}) \ln \frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}\]
此时得到的式子是一个不等式,确切的说是似然函数的下界。为了让似然函数达到最大,则需要得到合适的\(z,\theta\)让下界更高。
此时分两步来进行计算:第一步固定\(\theta\)调整\(Q_i(z^i)\),让下界上升至最高(前式的不等式取到等号),第二部固定\(Q_i(z^i)\)调整\(\theta\),使似然函数的值升高,下界达到最高,再重复第一步。循环往复直到第二步收敛。
E-step
根据琴生不等式,当X为常数时,肯定有\(E[f(X)]= f(EX)\),即
\[\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})} = c\]
而\(\sum_{z^{(i)}} Q_i(z^{(i)})=1\),因此
\[Q_i(z^{(i)})=\frac{p(x^{(i)},z^{(i)};\theta)}{\sum_z p(x^{(i)},z,\theta)}=p(x^{(i)},z^{(i)};\theta)\]
这就是第一步,让琴生不等式中的X为常数,取到f(x)的最大值。这一步记为E-step:
\[Q_i(z^{(i)}):=p(x^{(i)},z^{(i)};\theta)\]
M-step
固定\(\theta\),下界为
\[\sum^m_{i=1} \sum_{z^{(i)}} Q_i(z^{(i)}) \ln \frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}\]
此时要调整\(Q_i(z^i)\),让下界升到最高。记第t步为\(l(\theta^{t})\),第t+1步为\(l(\theta^{t+1})\)。由于下界在升高,最大似然函数值也会升高,\(Q_i(z^i)\)随之升高,直到收敛。因此可以推导
\[l(\theta^{(t+1)})=\sum^m_{i=1} \sum_{z^{(i)}} Q_i^{(t+1)}(z^{(i)}) \ln \frac{p(x^{(i)},z^{(i)};\theta^{(t+1)})}{Q^{(t+1)}_i(z^{(i)})}\\ \geq \sum^m_{i=1} \sum_{z^{(i)}} Q_i^{t}(z^{(i)}) \ln \frac{p(x^{(i)},z^{(i)};\theta^{(t+1)})}{Q^{t}_i(z^{(i)})}\\ \geq \sum^m_{i=1} \sum_{z^{(i)}} Q_i^{t}(z^{(i)}) \ln \frac{p(x^{(i)},z^{(i)};\theta^{t})}{Q^{t}_i(z^{(i)})}=l(\theta^{t})\]
最终得到
\[l(\theta^{(t+1)}) \geq l(\theta^t)\]
因此可得知M-step中,\(Q_i(z^i)\)的值会不断增加直到收敛。
M-step记为
\[\theta:=\arg \max_\theta \sum^m_{i=1} \sum_{z^{(i)}} Q_i(z^{(i)}) \ln \frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}\]
最终得到最大似然算法:
\[ \text{Repeat until convergence}\{ \\ \text{(E-step) For each i,set}\\ Q_i(z^{(i)}):=p(x^{(i)},z^{(i)};\theta) \\ \text{(M-step) set}\\ \theta:=\arg \max_\theta \sum^m_{i=1} \sum_{z^{(i)}} Q_i(z^{(i)}) \ln \frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}\\ \} \]
Reference
Stanford CS229 http://cs229.stanford.edu/notes/cs229-notes8.pdf cs229-notes8-EM算法.pdf 从最大似然到EM算法浅解 http://blog.csdn.net/zouxy09/article/details/8537620/