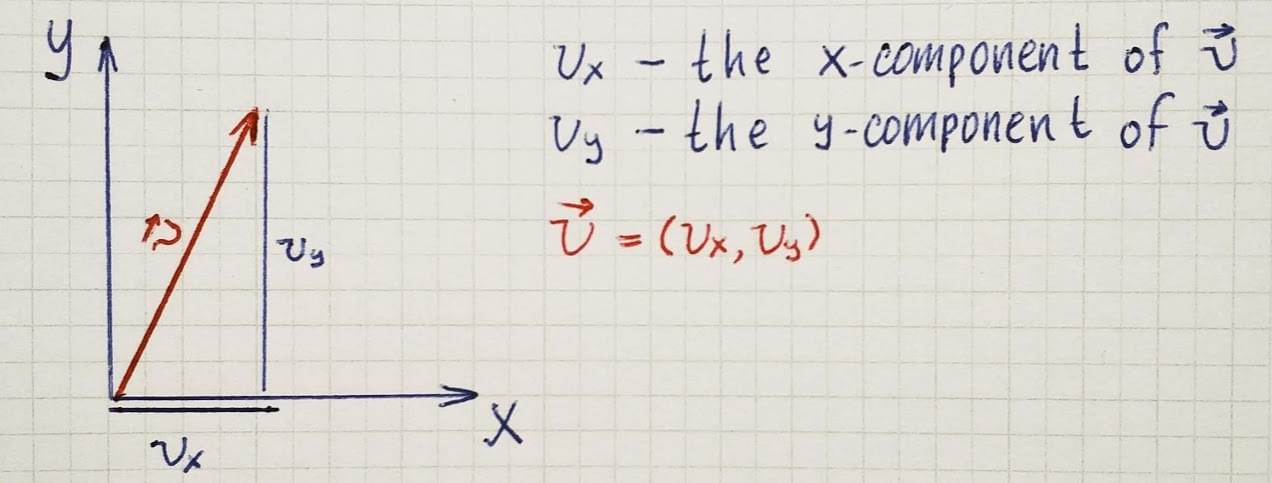本文是“JavaScript
线性代数”教程的一部分。
向量是用于精确表示空间中方向的方法。向量由一系列数值构成，每维数值都是向量的一个分量。在下图中，你可以看到一个由两个分量组成的、在
2 维空间内的向量。在 3 维空间内，向量会由 3 个分量组成。
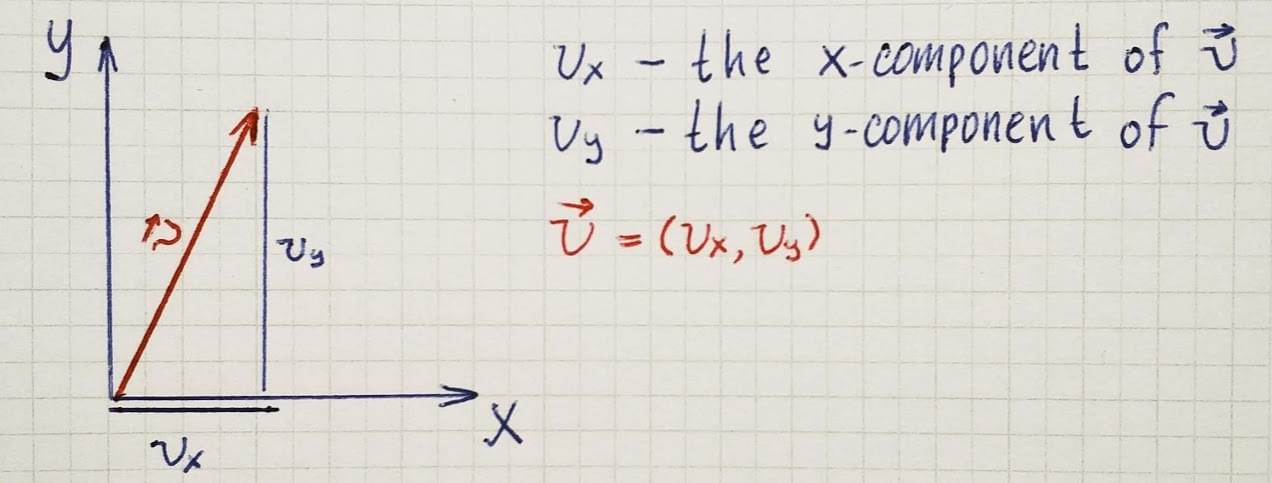the vector in 2D space
我们可以为 2 维空间的向量创建一个 Vector2D
类，然后为 3 维空间的向量创建一个 Vector3D
类。但是这么做有一个问题：向量并不仅用于表示物理空间中的方向。比如，我们可能需要将颜色（RGBA）表示为向量，那么它会有
4 个分量：红色、绿色、蓝色和 alpha
通道。或者，我们要用向量来表示有不同占比的 n
种选择（比如表示 5
匹马赛马，每匹马赢得比赛的概率的向量）。因此，我们会创建一个不指定维度的类，并像这样使用它：
1
2
3
4
5
6
7
8
9
10
| class Vector {
constructor(...components) {
this.components = components
}
}
const direction2d = new Vector(1, 2)
const direction3d = new Vector(1, 2, 3)
const color = new Vector(0.5, 0.4, 0.7, 0.15)
const probabilities = new Vector(0.1, 0.3, 0.15, 0.25, 0.2)
|
向量运算
考虑有两个向量的情况，可以对它们定义以下运算：
basic vector operations
其中，α ∈ R 为任意常数。
我们对除了叉积之外的运算进行了可视化，你可以在此处找到相关示例。此 GitHub
仓库里有用来创建这些可视化示例的 React
项目和相关的库。如果你想知道如何使用 React 和 SVG
来制作这些二维可视化示例，请参考本文。
加法与减法
与数值运算类似，你可以对向量进行加法与减法运算。对向量进行算术运算时，可以直接对向量各自的分量进行数值运算得到结果：
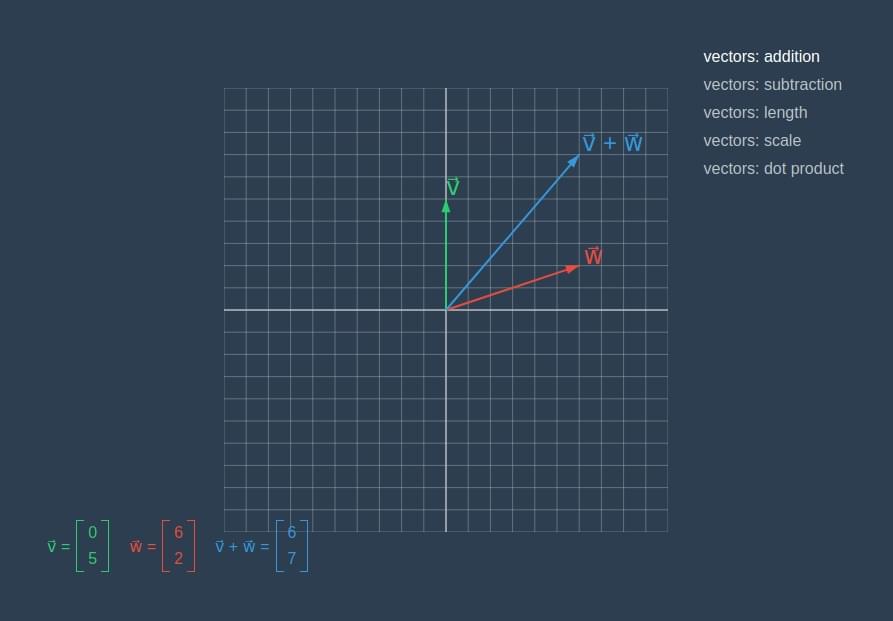vectors addition
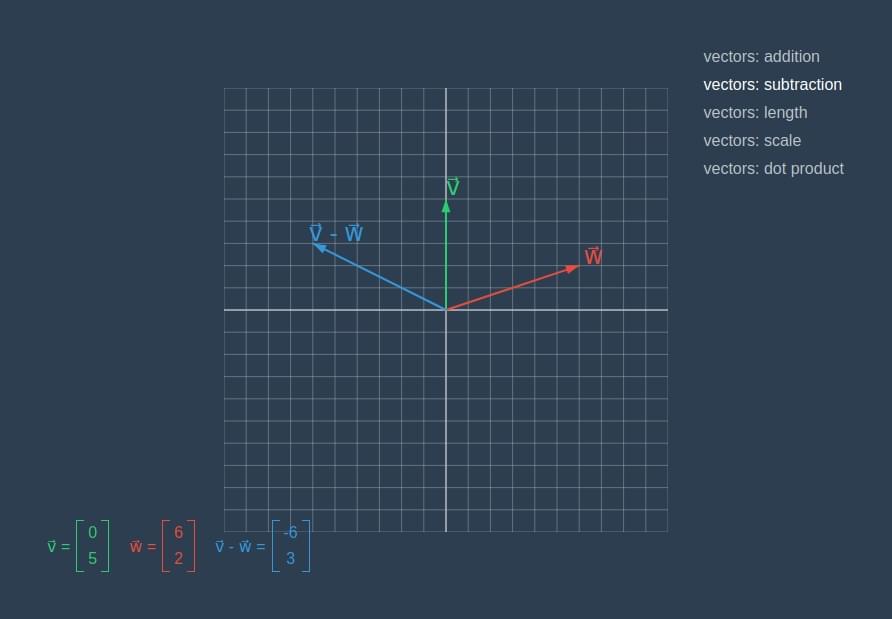vectors subtraction
加法函数接收另一个向量作为参数，并将对应的向量分量相加，返回得出的新向量。减法函数与之类似，不过会将加法换成减法：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| class Vector {
constructor(...components) {
this.components = components
}
add({ components }) {
return new Vector(
...components.map((component, index) => this.components[index] + component)
)
}
subtract({ components }) {
return new Vector(
...components.map((component, index) => this.components[index] - component)
)
}
}
const one = new Vector(2, 3)
const other = new Vector(2, 1)
console.log(one.add(other))
console.log(one.subtract(other))
|
缩放
我们可以对一个向量进行缩放，缩放比例可为任意数值 α ∈
R。缩放时，对所有向量分量都乘以缩放因子 α。当
α > 1 时，向量会变得更长；当 0 ≤ α <
1 时，向量会变得更短。如果 α
是负数，缩放后的向量将会指向原向量的反方向。
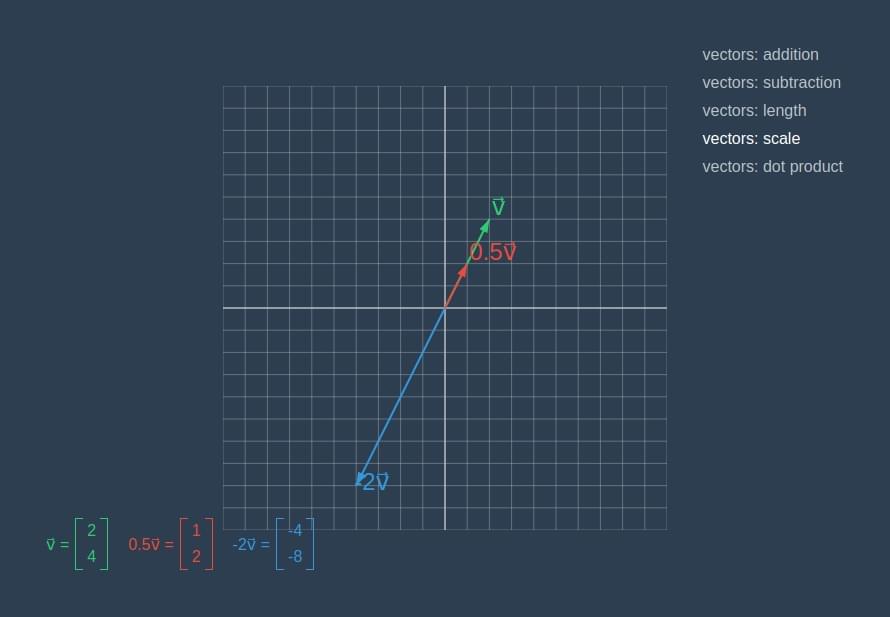scaling vector
在 scaleBy
方法中，我们对所有的向量分量都乘上传入参数的数值，得到新的向量并返回：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| class Vector {
constructor(...components) {
this.components = components
}
scaleBy(number) {
return new Vector(
...this.components.map(component => component * number)
)
}
}
const vector = new Vector(1, 2)
console.log(vector.scaleBy(2))
console.log(vector.scaleBy(0.5))
console.log(vector.scaleBy(-1))
|
长度
向量长度可由勾股定理导出：
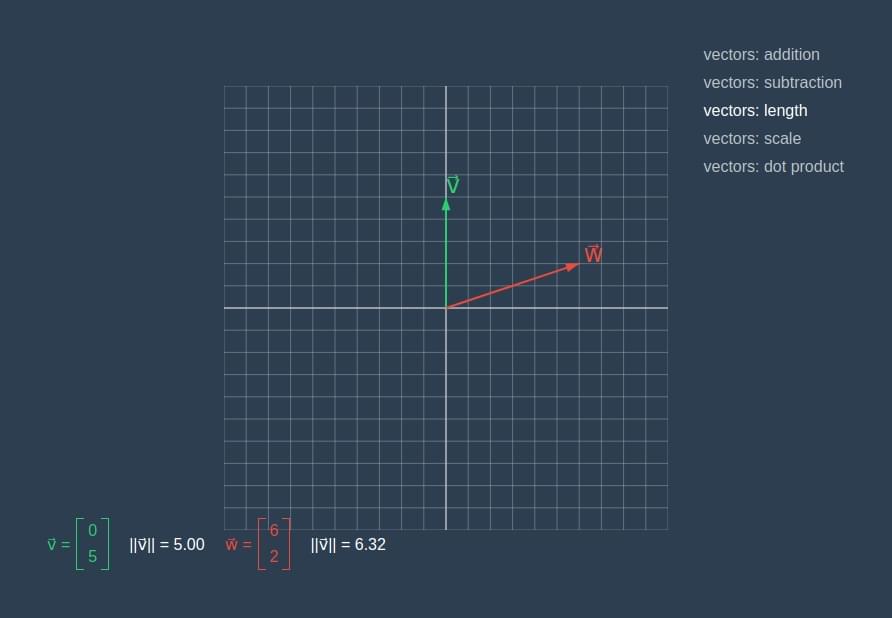vectors length
由于在 JavaScript 内置的 Math
对象中有现成的函数，因此计算长度的方法非常简单：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| class Vector {
constructor(...components) {
this.components = components
}
length() {
return Math.hypot(...this.components)
}
}
const vector = new Vector(2, 3)
console.log(vector.length())
|
点积
点积可以计算出两个向量的相似程度。点积方法接收两个向量作为输入，并输出一个数值。两个向量的点积等于它们各自对应分量的乘积之和。
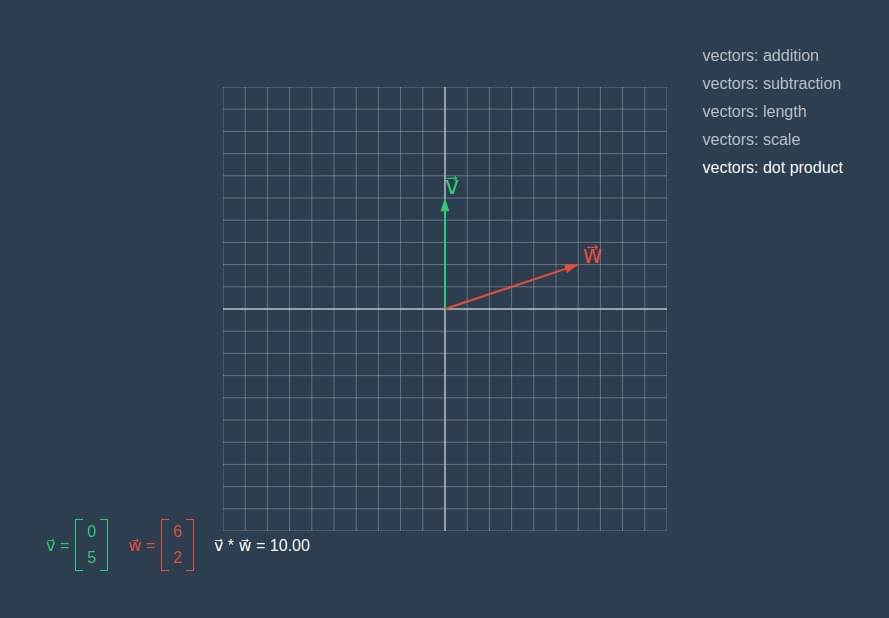dot product
在 dotProduct 方法中，接收另一个向量作为参数，通过
reduce 方法来计算对应分量的乘积之和：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| class Vector {
constructor(...components) {
this.components = components
}
dotProduct({ components }) {
return components.reduce((acc, component, index) => acc + component * this.components[index], 0)
}
}
const one = new Vector(1, 4)
const other = new Vector(2, 2)
console.log(one.dotProduct(other))
|
在我们观察几个向量间的方向关系前，需要先实现一种将向量长度归一化为 1
的方法。这种归一化后的向量在许多情景中都会用到。比如说当我们需要在空间中指定一个方向时，就需要用一个归一化后的向量来表示这个方向。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| class Vector {
constructor(...components) {
this.components = components
}
normalize() {
return this.scaleBy(1 / this.length())
}
}
const vector = new Vector(2, 4)
const normalized = vector.normalize()
console.log(normalized)
console.log(normalized.length())
|
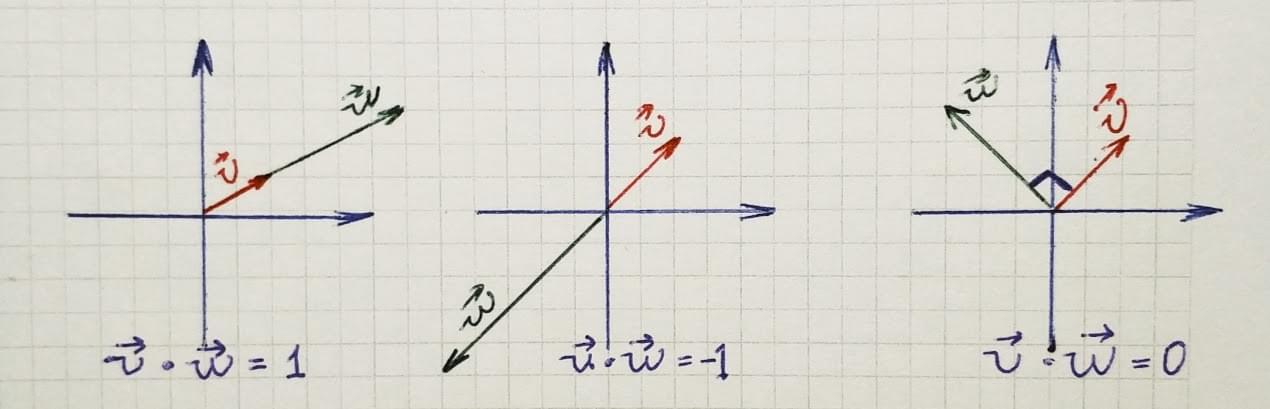using dot product
如果两个归一化后的向量的点积结果等于
1，则意味着这两个向量的方向相同。我们创建了 areEqual
函数用来比较两个浮点数：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| const EPSILON = 0.00000001
const areEqual = (one, other, epsilon = EPSILON) =>
Math.abs(one - other) < epsilon
class Vector {
constructor(...components) {
this.components = components
}
haveSameDirectionWith(other) {
const dotProduct = this.normalize().dotProduct(other.normalize())
return areEqual(dotProduct, 1)
}
}
const one = new Vector(2, 4)
const other = new Vector(4, 8)
console.log(one.haveSameDirectionWith(other))
|
如果两个归一化后的向量点积结果等于 -1，则表示它们的方向完全相反：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| class Vector {
constructor(...components) {
this.components = components
}
haveOppositeDirectionTo(other) {
const dotProduct = this.normalize().dotProduct(other.normalize())
return areEqual(dotProduct, -1)
}
}
const one = new Vector(2, 4)
const other = new Vector(-4, -8)
console.log(one.haveOppositeDirectionTo(other))
|
如果两个归一化后的向量的点积结果为
0，则表示这两个向量是相互垂直的：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| class Vector {
constructor(...components) {
this.components = components
}
isPerpendicularTo(other) {
const dotProduct = this.normalize().dotProduct(other.normalize())
return areEqual(dotProduct, 0)
}
}
const one = new Vector(-2, 2)
const other = new Vector(2, 2)
console.log(one.isPerpendicularTo(other))
|
叉积
叉积仅对三维向量适用，它会产生垂直于两个输入向量的向量：
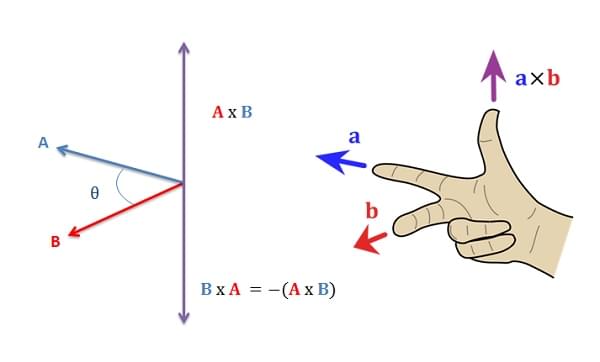
我们实现叉积时，假定它只用于计算三维空间内的向量。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| class Vector {
constructor(...components) {
this.components = components
}
crossProduct({ components }) {
return new Vector(
this.components[1] * components[2] - this.components[2] * components[1],
this.components[2] * components[0] - this.components[0] * components[2],
this.components[0] * components[1] - this.components[1] * components[0]
)
}
}
const one = new Vector(2, 1, 1)
const other = new Vector(1, 2, 2)
console.log(one.crossProduct(other))
console.log(other.crossProduct(one))
|
其它常用方法
在现实生活的应用中，上述方法是远远不够的。比如说，我们有时需要找到两个向量的夹角、将一个向量反向，或者计算一个向量在另一个向量上的投影等。
在开始编写上面说的方法前，需要先写下面两个函数，用于在角度与弧度间相互转换：
1
2
| const toDegrees = radians => (radians * 180) / Math.PI
const toRadians = degrees => (degrees * Math.PI) / 180
|
夹角
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| class Vector {
constructor(...components) {
this.components = components
}
angleBetween(other) {
return toDegrees(
Math.acos(
this.dotProduct(other) /
(this.length() * other.length())
)
)
}
}
const one = new Vector(0, 4)
const other = new Vector(4, 4)
console.log(one.angleBetween(other))
|
反向
当需要将一个向量的方向指向反向时，我们可以对这个向量进行 -1
缩放：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| class Vector {
constructor(...components) {
this.components = components
}
negate() {
return this.scaleBy(-1)
}
}
const vector = new Vector(2, 2)
console.log(vector.negate())
|
投影
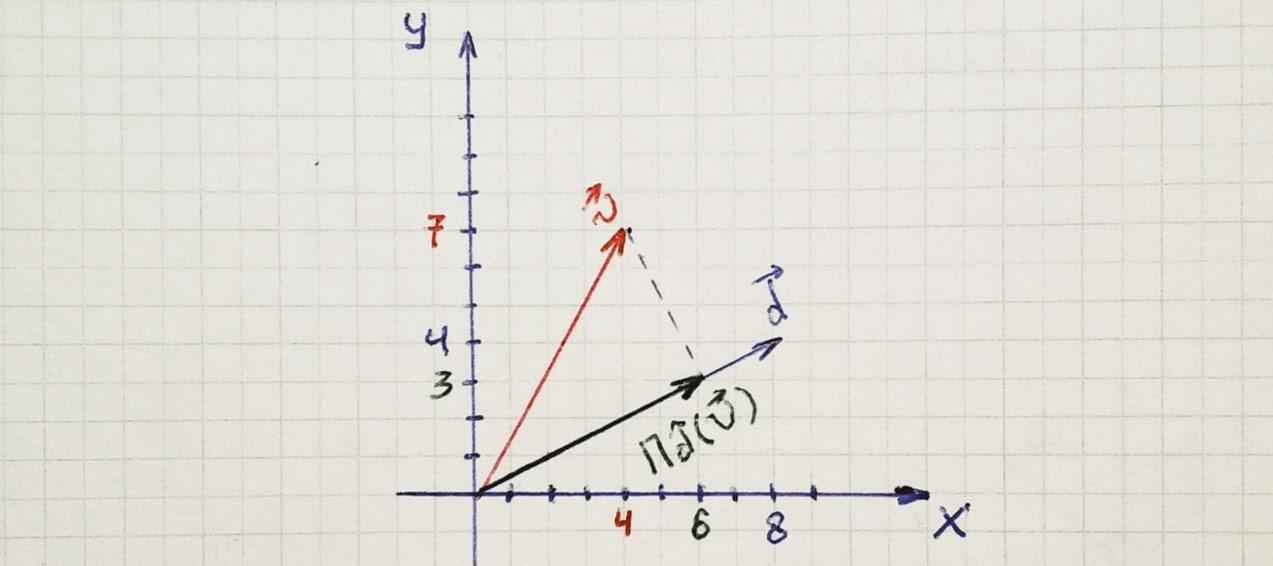project v on d
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| class Vector {
constructor(...components) {
this.components = components
}
projectOn(other) {
const normalized = other.normalize()
return normalized.scaleBy(this.dotProduct(normalized))
}
}
const one = new Vector(8, 4)
const other = new Vector(4, 7)
console.log(other.projectOn(one))
|
设定长度
当需要给向量指定一个长度时，可以使用如下方法：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| class Vector {
constructor(...components) {
this.components = components
}
withLength(newLength) {
return this.normalize().scaleBy(newLength)
}
}
const one = new Vector(2, 3)
console.log(one.length())
const modified = one.withLength(10)
console.log(modified.length())
|
判断相等
为了判断两个向量是否相等，可以对它们对应的分量使用
areEqual 函数：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| class Vector {
constructor(...components) {
this.components = components
}
equalTo({ components }) {
return components.every((component, index) => areEqual(component, this.components[index]))
}
}
const one = new Vector(1, 2)
const other = new Vector(1, 2)
console.log(one.equalTo(other))
const another = new Vector(2, 1)
console.log(one.equalTo(another))
|
单位向量与基底
我们可以将一个向量看做是“在 x 轴上走 \(v_x\) 的距离、在 y 轴上走 \(v_y\) 的距离、在 z 轴上走 \(v_z\) 的距离”。我们可以使用 \(\hat { \imath }\) 、\(\hat { \jmath }\) 和 \(\hat { k }\)
分别乘上一个值更清晰地表示上述内容。下图分别是 \(x\)、\(y\)、\(z\)
轴上的单位向量：
\[
\hat { \imath } = ( 1,0,0 ) \quad \hat { \jmath } = ( 0,1,0 ) \quad \hat
{ k } = ( 0,0,1 )\]
任何数值乘以 \(\hat { \imath }\)
向量，都可以得到一个第一维分量等于该数值的向量。例如：
\[
2 \hat { \imath } = ( 2,0,0 ) \quad 3 \hat { \jmath } = ( 0,3,0 ) \quad
5 \hat { K } = ( 0,0,5 )
\]
向量中最重要的一个概念是基底。设有一个 3 维向量
\(\mathbb{R}^3\)，它的基底是一组向量：\(\{\hat{e}_1,\hat{e}_2,\hat{e}_3\}\)，这组向量也可以作为
\(\mathbb{R}^3\) 的坐标系统。如果 \(\{\hat{e}_1,\hat{e}_2,\hat{e}_3\}\)
是一组基底，则可以将任何向量 \(\vec{v} \in
\mathbb{R}^3\) 表示为该基底的系数 \((v_1,v_2,v_3)\)：
\[
\vec{v} = v_1 \hat{e}_1 + v_2 \hat{e}_2 + v_3 \hat{e}_3
\]
向量 \(\vec{v}\) 是通过在 \(\hat{e}_1\) 方向上测量 \(v_2\) 的距离、在 \(\hat{e}_2\) 方向上测量 \(v_1\) 的距离、在 \(\hat{e}_3\) 方向上测量 \(v_3\) 的距离得出的。
在不知道一个向量的基底前，向量的系数三元组并没有什么意义。只有知道向量的基底，才能将类似于
\((a,b,c)\)
三元组的数学对象转化为现实世界中的概念（比如颜色、概率、位置等）。