关键词规则生成
概述
提取关键词将得到一系列的词库,要将这些词应用于文本筛查、分类则必须要对这些词进行拆分、组合,形成特定的规则,再应用这些规则对文本进行匹配,得到某文本所对应的模式。
要生成规则,即需要从系列关键词通过某些算法找出在不同样本文本下关键词的共有特征(或规律),再对多种特征(或规律)进行组合得到某种策略,最终通过策略对目标文本进行判定。因此关键词规则生成可以总结为以下几个主要步骤:
- 关键词特征或规律查找
- 策略生成
- 策略优化与化简
对于关键词特征与规律的查找,可以视为机器学习中的分类问题的反向过程。分类问题简要来说即给定标注样本,通过特征训练,得到一个可适用于同类样本的分类策略。常用的分类方法包括决策树、SVM、神经网络等方法。
决策树算法是常用的数据分类算法。决策树算法具有以下优点:
- 决策树算法中学习简单的决策规则建立决策树模型的过程非常容易理解
- 决策树模型可以可视化,非常直观
- 应用范围广,可用于分类和回归,而且非常容易做多类别的分类
- 能够处理数值型和连续的样本特征
由于它生成分类策略的可解释性,以及树状结构的可编辑性,在本步骤中可选用决策树算法作为样本分类策略。
下图为对某样本文本进行决策树(CART)生成的分类器策略可视化图像:

可以从图片中看出,决策树算法根据样本标注训练而成了对应的基于关键词的文本分类器。此分类器策略为清晰的树状结构,每个节点代表一个判断条件,每个树杈代表一个条件分支。为了得到在特定计算性能高、可解释性更好的策略,需要对其进行进一步的策略挖掘及精简。
由于决策树得到的策略为树状结构,因此在这种结构上的进一步策略挖掘可选用盲目搜索算法;又由于此模型为树状结构,最终分类落于叶子节点中,故采用深度优先搜索(DFS)对此树的路径进行检索,进一步优化策略。
在决策树得到的规则通过深度优先搜索之后,会得到一系列的组别,每个组别中包含各个关键词的“与”和“或”两种逻辑关系。在目标文本中使用时,即可通过这些逻辑关系的匹配找出对应的模式。
但由于决策树得到的策略叶子节点通常较多(如上图所示),通过深度优先搜索得到的策略也非常繁杂,最终生成得到的规则也会非常复杂,因此还可以进行进一步的策略化简。
在此步骤中,实质上是对多个逻辑代数运算及逻辑代数复合运算组合而成的逻辑函数进行化简。逻辑函数的化简方法一般有如下三种:
- 公式化简法
- 卡诺图法
- Q-M 法
由于在此步骤实际应用时逻辑规则较为繁杂,且“与”—“或”逻辑对较多,比起公式化简法或卡诺图法,Q-M 算法在选取出可以覆盖逻辑规则真值的最小质蕴涵项时更能发挥优势。
最终,通过决策树算法生成树、对决策树进行深度优先搜索得到包含“与”、“或”的分类逻辑、对分类逻辑应用 Q-M 算法,最终得到了包含“与”、“或”、“非”三种逻辑关系的可解释性强、精简的规则。
决策树
决策树是一个树结构,其每个非叶节点表示一个特征属性上的测试,每个分支代表这个特征属性在某个值域上的输出,而每个叶节点存放一个类别。运用决策树进行决策的过程就是从根节点开始,测试待分类项中相应的特征属性,并按照其值选择输出分支,直到到达叶子节点,将叶子节点存放的类别作为决策结果。
决策树算法是一种逼近离散函数值的方法。它是一种典型的分类方法,首先对数据进行处理,利用归纳算法生成可读的规则和决策树,然后使用决策对新数据进行分析。本质上决策树算法是通过一系列规则对数据进行分类的过程。
决策树算法构造决策树来发现数据中蕴涵的分类规则.如何构造精度高、规模小的决策树是决策树算法的核心内容。决策树构造可以分两步进行:
第一步,决策树的生成:由训练样本集生成决策树的过程。一般情况下,训练样本数据集是根据实际需要有历史的、有一定综合程度的,用于数据分析处理的数据集。
第二步,决策树的剪枝:决策树的剪枝是对上一阶段生成的决策树进行检验、校正和修下的过程,主要是用新的样本数据集(称为测试数据集)中的数据校验决策树生成过程中产生的初步规则,将那些影响预衡准确性的分枝剪除。
在第一步决策树的生成中,需要确定树杈的分裂属性(即在多个自变量中,优先选择哪个自变量进行分叉)。而采用何种计算方式选择树杈决定了决策树算法的类型,典型的分裂属性的选择的方法有 ID3 算法、C4.5 算法、CART 算法三种,三种决策树算法选择树杈的方式是不一样的。
ID3 算法
ID3 算法是目前决策树算法中较有影响力的算法,于 1986 年由 Quinlan 提出。该算法只是一个启发式算法。ID3 算法的核心是判断测试哪个属性为最佳的分类属性。ID3 算法选择分裂后信息增益最大的属性进行分裂,以信息增益度量属性选择。ID3 算法中常用到的两个概念是熵和信息增益。
熵是刻画任意样本例集的纯度,如果目标属性具有 m 个不同的值,那么 D 相对于 m 这个状态的分类的熵定义为:
\[ \text{inf}\ o(D) = -\sum^m_{i=1}p_i \log_2 (P_i) \]
其中 Pi 表示 Pi 是 m 类别的比例。
一个属性的信息增益就是由于使用这个属性分割样例而导致的期望熵降低,更精确来讲,一个属性A相对样本例集合S的信息增益 Gain(S,A) 被定义为:
\[ gain(A) = info(D) - infoA(D) \]
A 对 D 划分的期望信息为:
\[ \text{inf}\ o_A(D) = \sum^v_{j=1} \frac{|D_j|}{|D|} \text{inf}\ o(D_j) \]
ID3 算法不足之处是只能处理离散型数据,信息增益的选择分裂属性的方式会偏向选择具有大量值得属性。
C4.5 算法
ID3 算法在实际应用中存在一些问题,于是 Quilan 在保留 ID3 算法优点基础上提出了 C4.5 算法,C4.5 算法只是 ID3 算法的改进算法。C4.5 算法采用最大信息增益率的属性被选为分裂属性。C4.5 算法中用到了“分裂信息”这一概念,该概念可以表示为:
\[ split\_ \text{inf}\ o_A(D) = -\sum^v_{j=1} \frac{|D_j|}{|D|} \log_2\frac{|D_j|}{|D|} \]
信息增益率的定义是:
\[ gain\_ratio(A) = \frac{gainA}{split\_\text{inf}\ o(A)} \]
C4.5 算法是对 ID3 算法的一种改进,改进后可以计算连续型属性的值。对于连续型属性的值,只需将连续型变量由小到大递增排序,取相邻连个值的中点作为分裂点,然后按照离散型变量计算信息增益的方法计算信息增益,取其中最大的信息增益作为最终的分裂点。
C4.5 算法继承了 ID3 算法的优点,并在以下几方面对 ID3 算法进行了改进:
用信息增益率来选择属性,克服了用信息增益选择属性时偏向选择取值多的属性的不足;
在树构造过程中进行剪枝;
能够完成对连续属性的离散化处理;能够对不完整的数据进行处理。
CART 算法
CART 算法选择分裂属性的方式首先要计算不纯度,然后利用不纯度计算 Gini 指标,然后计算有效子集的不纯度和 Gini 指标,选择最小的 Gini 指标作为分裂属性。
\[ Gini(D) = 1 - \sum^n_{i=0}(\frac{Di}{D})^2 \]
\[ Gini(D|A) = \sum^n_{i=0} \frac{Di}{D} Gini(D i)\]
由于 CART 算法在处理离散数据上具有优势,因此对于关键词规则的生成可选用此方法生成决策树。
深度优先搜索算法
搜索算法可分为盲目搜索算法和启发式搜索算法两种,二者的区别在于:启发式搜索算法的每一步都试图向着目标状态方向进行搜索,而盲目搜索算法则是每一步按照固定的规则进行搜索,然后判断是否达到目标状态。相比之下,启发式搜索算法克服了盲目搜索算法的盲目性问题。
虽然启发式搜索算法可以解决盲目搜索算法的盲搜索问题,但是在实际问题求解中,缺少一些必要的信息来构建启发式搜索算法,此时采用盲目搜索算法仍然是解决问题的有效手段。盲目搜索算法有两种:一种按照广度优先展开搜索树的搜索算法,叫广度优先搜索法;另一种则是按照深度优先展开搜索的搜索算法,叫深度优先搜索法算法。
深度优先搜索算法是优先扩展尚未扩展的且具有最大深度的节点;广度优先搜索法是在扩展完第 K 层的节点后才扩展 K+1 层的节点。在此应用深度优先搜索算法。
假设初始状态是图中所有顶点未曾被访问,从图中某个顶点 i 出发,访问此顶点,然后依次从 i 的未被访问的邻接点出发深度优先遍历图,直至图中所有和 i 有路径的顶点都被访问为止。若此时图中尚有顶点未被访问,则另选图中未曾访问的顶点为起始点,重复上述过程,直至图中所有顶点都被访问为止。在节点遍历过程中,应该注意节点的回溯搜索以及避免节点被重复搜索。
在搜索过程中,如何避免被搜过的节点不被重复搜索以及节点的回溯是主要难点。根据关联矩阵以及深度优先搜索算法,从节点 i 搜索出节点 j,如果节点 j 已经被搜索过,那么修改关联矩阵中对应节点 i 和节点 j 的元素为 0,并返回节点 i 重新搜索与之相联的另一节点。当节点 j 是该条树枝的最后一个节点时,修改关联矩阵中相应的元素,并且返回节点 i 重新搜索与之相连的另一树枝。依此类推,直至遍历所有节点,也就是关联矩阵的所有元素都变为 0 时,停止搜索。在遍历各节点的同时,根据节点的先后顺序以及树枝集合,合理地安排各节点坐标。其搜索过程逻辑如下图所示:
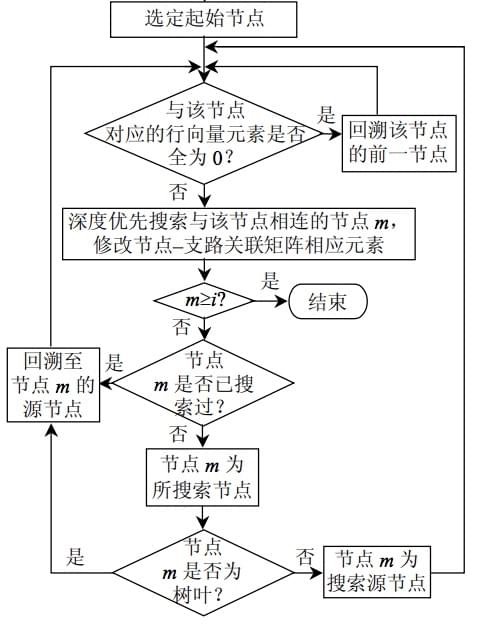
Q-M 算法
在得到只包含“与”、“或”的逻辑函数之后,可对逻辑进行更进一步的简化与合并,并加上“非”逻辑来使得逻辑函数更具解释性。
下图为一个简单逻辑函数的卡诺图,101 项被覆盖了 3 次,明显可对函数进行化简。
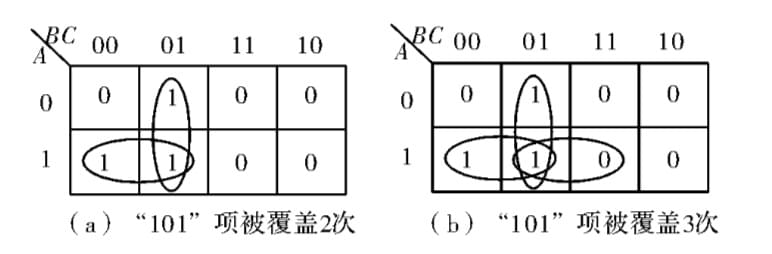
Q-M 算法是由 Quine 和 Mccluskey 提出的一种系统列表化简法。这种化简方法和卡诺图化简法的基本思想大致相同, 是通过找出函数 F 的全部质蕴涵项、必要质蕴涵项以及最简质蕴涵项集来求得最简表达式。
下面为蕴含项与质蕴涵项的定义:
蕴涵项:在函数的“与”—“或”表达式中,每个“与”项被称为该函数的蕴涵项。显然在函数卡诺图中,任何一个 1 方格所对应的最小项或者卡诺圈中的 \(2^n\) 个 1 方格所对应的“与”项都是函数的蕴涵项。
质蕴涵项:若函数的一个蕴涵项不是该函数中其它蕴涵项的子集,则此蕴涵项称为质蕴涵项,简称为质项。显然在函数卡诺图中,按照最小项合并规律,如果某个卡诺圈不可能被其它更大的卡诺圈包含,那么该卡诺圈所对应的“与”项为质蕴涵项。
必要质蕴涵项:若函数的一个质蕴涵项所包含的某一个最小项不被函数的其它任何质蕴涵项包含,则此质蕴涵项被称为必要质蕴涵项,简称为必要质项。在函数卡诺图中,若某个卡诺圈包含了不可能被任何其它卡诺圈包含的 1 方格,那么该卡诺圈所对应的“与”项为必要质蕴涵项。
一般的化简步骤是:
第一步:将函数表示成“最小项之和”形式,并用二进制码表示每—个最小项。
第二步:找出函数的全部质蕴涵项。先将 n 个变量函数中的相邻最小项合并,消去相异的—个变量,得到 (n-1) 个变量的“与”项,再将相邻的 (n-1) 个变量的“与”项合并,消去相异的变量,得到 (n-2) 个变量的“与”项。依此类推,直到不能再合并为止。所得到的全部不能再合并的“与”项(包括不能合并的最小项),即所要求的全部质蕴涵项。
第三步:找出函数的必要质蕴涵项。
第四步:找出函数的最小覆盖。