编辑距离及编辑距离算法

Posted on In

编辑距离又称为 Levenshtein 距离，指两个字串之间，由一个转成另一个所需的最少编辑操作次数。操作包括将一个字符替换成另一个字符，插入一个字符，删除一个字符。一般来说，编辑距离越小，两个串的相似度越大。（cite from baidu baike）

最小编辑距离在应用中常作为一种相似度计算方法。例如DNA分析、拼写纠错（Spell correction）、命名实体抽取（Named Entity Extraction）、实体共指（Entity Conference）、识别平行网页等。

计算某两个字符串的编辑距离时，可以列下面的表：（如 apple 与 people）

0 p e o p l e
0 0 1 2 3 4 5 6
a 1
p 2
p 3
l 4
e 5

从上到下，从左到右遍历，对于每一个空来说，它的值为：

  • 左边数字 +1
  • 上面数字 +1
  • 如对应的行头与列头的字母相等，则取左上角的数字；否则取左上角数字 +1

这三者的最小值。反复遍历，如下所示：

0 p e o p l e
0 0 1 2 3 4 5 6
a 1 1 2 3 4 5 6
p 2
p 3
l 4
e 5
0 p e o p l e
0 0 1 2 3 4 5 6
a 1 1 2 3 4 5 6
p 2 1 2 3 3 4 5
p 3
l 4
e 5
0 p e o p l e
0 0 1 2 3 4 5 6
a 1 1 2 3 4 5 6
p 2 1 2 3 3 4 5
p 3 2 2 3 3 4 5
l 4
e 5
0 p e o p l e
0 0 1 2 3 4 5 6
a 1 1 2 3 4 5 6
p 2 1 2 3 3 4 5
p 3 2 2 3 3 4 5
l 4 3 3 3 4 3 4
e 5
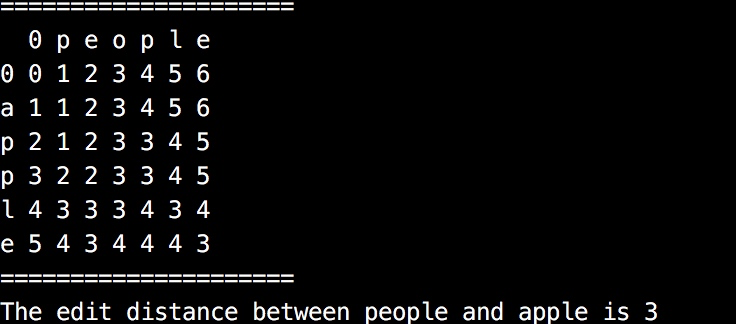
0 p e o p l e
0 0 1 2 3 4 5 6
a 1 1 2 3 4 5 6
p 2 1 2 3 3 4 5
p 3 2 2 3 3 4 5
l 4 3 3 3 4 3 4
e 5 4 3 4 4 4 3

右下角数字为 3，则 apple 与 people 的编辑距离为 3。

代码： 根据以上自然语言的描述，可以直接利用遍历写出相应代码。如下所示：

1
2
3
4
5
6
7
8
9
10
11
12
13

def literation(matrix):
    for i in range(2, len(matrix)):
        for j in range(2, len(matrix[0])):
            up_num = matrix[i - 1][j]
            left_num = matrix[i][j - 1]
            left_up_num = matrix[i - 1][j - 1]
            if matrix[0][j] != matrix[i][0]:
                left_up_num += 1
            matrix[i][j] = min(up_num + 1, left_num + 1, left_up_num)
            print_matrix(matrix)
    return matrix

完整代码放在 github 上

运行结果如下：

upload successful