python实现k-means分类算法

Posted on 2017-03-22 In Algorithm

准备实现一些算法，顺带复习numpy，因此将比较简单的k-means算法用python实现一次。

k-means算法

准备数据集

首先，考虑数据集来源。懒得去找数据，因此直接用scikit的dataset模块随机生成一组聚类数据。既然要生成聚类数据，用make_blobs是再好不过了。sklearn.dataset.make_blobs文档

为了直观地展示数据，用matplotlib来进行数据可视化。

import numpy as np
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt

def generateDataAndShow():
    plt.figure(figsize=(8,5))
    plt.title("Dataset", fontsize='small')
    datas, class_info = make_blobs(n_samples=200 ,n_features=2, centers=3)
    plt.scatter(datas[:, 0], datas[:, 1], marker='o', c=class_info)
    plt.show()
    return datas

if __name__=='__main__':
    data = generateDataAndShow()

可以得到一个有三个聚类，共200个点的数据集。如图所示

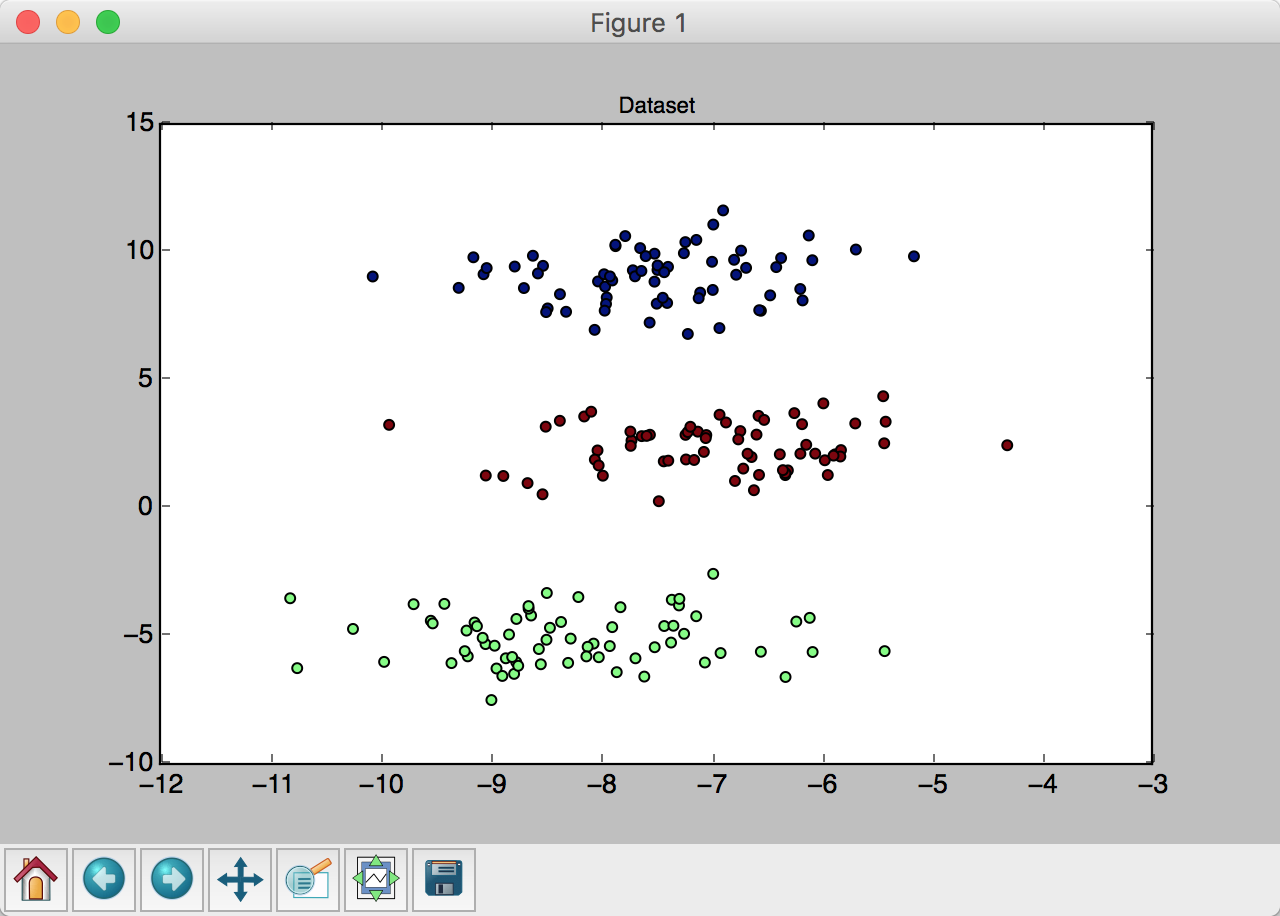
且每次运行都会生成不同的数据。

此时，得到200对坐标数据以及相应的分类数据。仅将坐标数据拿出来进行计算。

算法实现

1、随机生成3个点，作为初始聚类中心。为了减少计算量，所以将3个点生成在所有点的值域中。此时data的数据结构是Float[][]，第一重数组为一个点，第二重数组为点的两个坐标。因此需要用到numpy的amax函数与amin函数：

1	[x_max, y_max], [x_min, y_min] = np.amax(data,axis=0),np.amin(data,axis=0)

使用numpy.random的rand生成一组点：

1
2
3

centers = np.random.rand(3,2)
centers[0:,0] = (x_max-x_min)*centers[0:,0]+x_min
centers[0:,1] = (y_max-y_min)*centers[0:,1]+y_min

这样就得到了在值域内的3个随机点。

2、计算距离。二维平面内两个点的距离公式为

\[d=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}\]

因此可以计算出每个点分别到三个聚类中心的距离：

def distance(data, dots):
    rs = []
    for d in data:
        rs.append([])
        for dot in dots:
            rs[-1].append(((d[0]-dot[0])**2+(d[1]-dot[1])**2)**0.5)
    return rs

3、分组。根据计算得到的各个点距离聚类中心的距离，可以判断这个点是属于哪一个聚类的。

1 2	def classify(dis): return [i.index(min(i)) for i in dis]

返回一个分类索引数组。这个时候也可以用plt将此时的分类打印出来，和最开始的正确聚类对比一下：

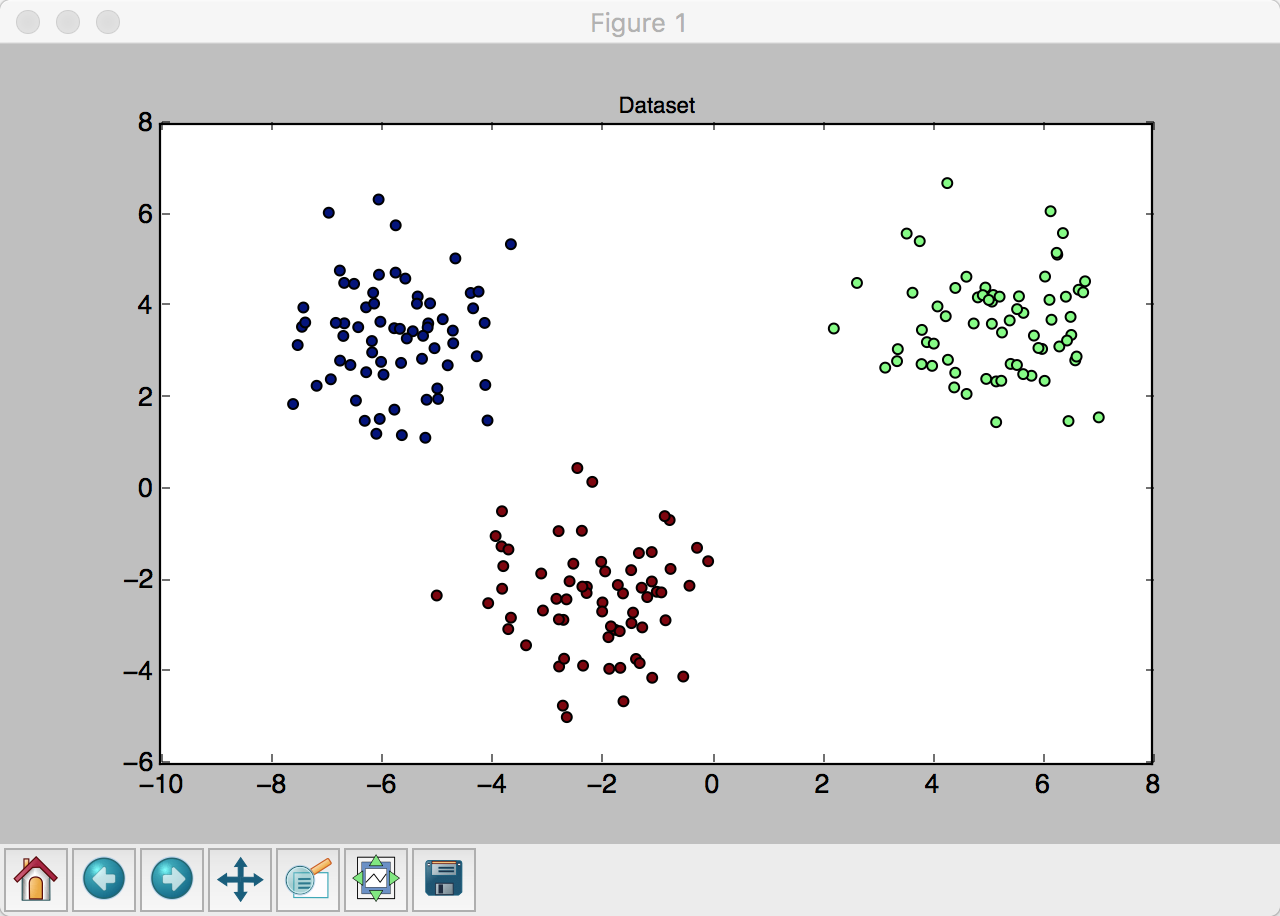
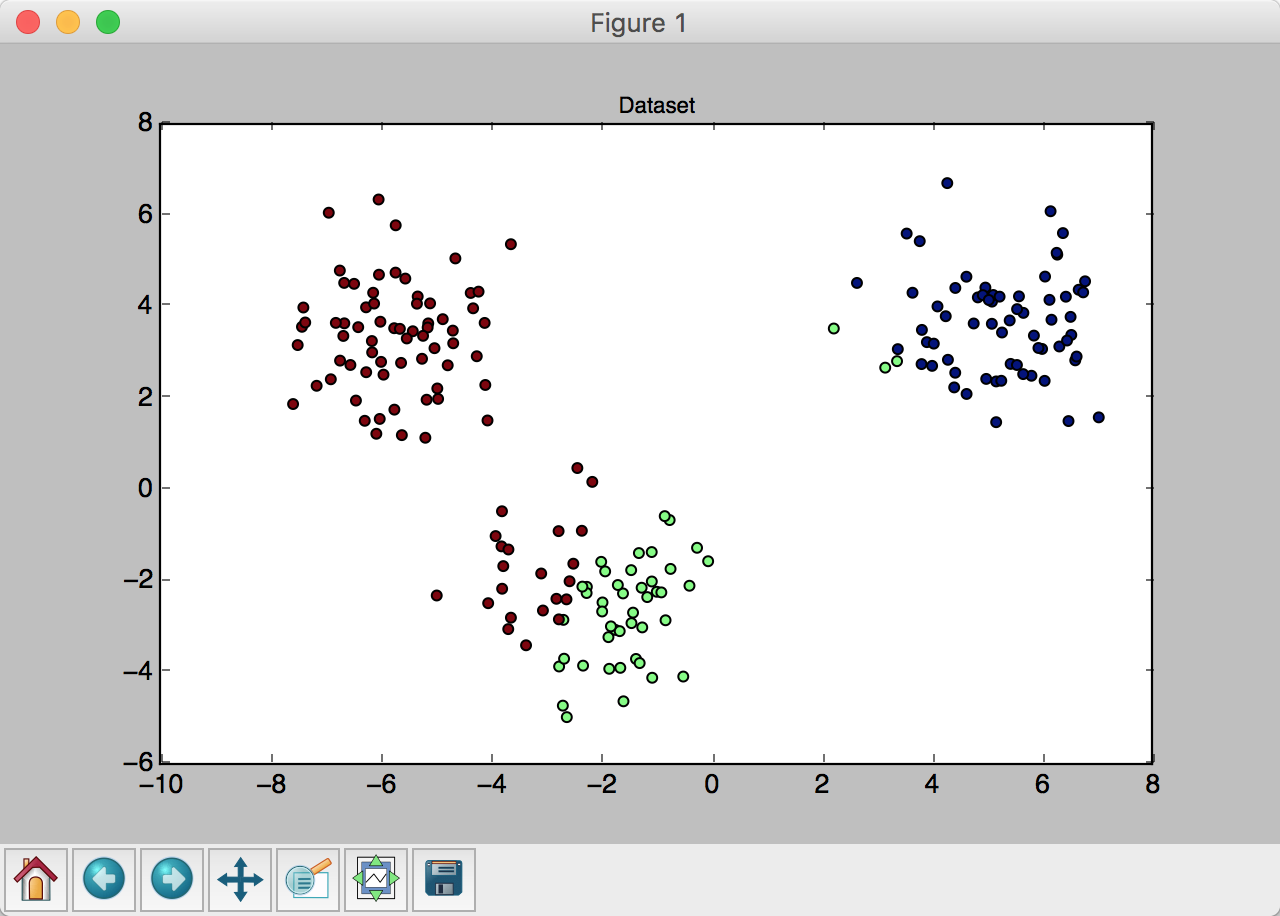
考虑一种特殊情况：只分出两个聚类。这时候将无法继续计算下去，应当重新随机生成中心。

4、移动聚类中心。根据随机得到的初始聚类，重新计算每个聚类的质心作为其新的聚类中心。

def calCenters(data, clazz):
    clz = [[] for i in range(3)]
    for index,dot in enumerate(data):
        clz[clazz[index]].append(dot)
    return [sum(x)/len(x) for x in clz]

得到了新的聚类中心

5、循环上述步骤，直到收敛。

while True:
    new_centers = calCenters(data, clazz)
    if equal(new_centers,centers):break
    else:
        centers = new_centers
        clazz = classify(distance(data,centers))

收敛条件是聚类中心点不再变化。

最终代码：https://github.com/lsvih/algorithm-practice/blob/master/k-means/k-means.py (_src=undefined)

结果

生成的聚类：

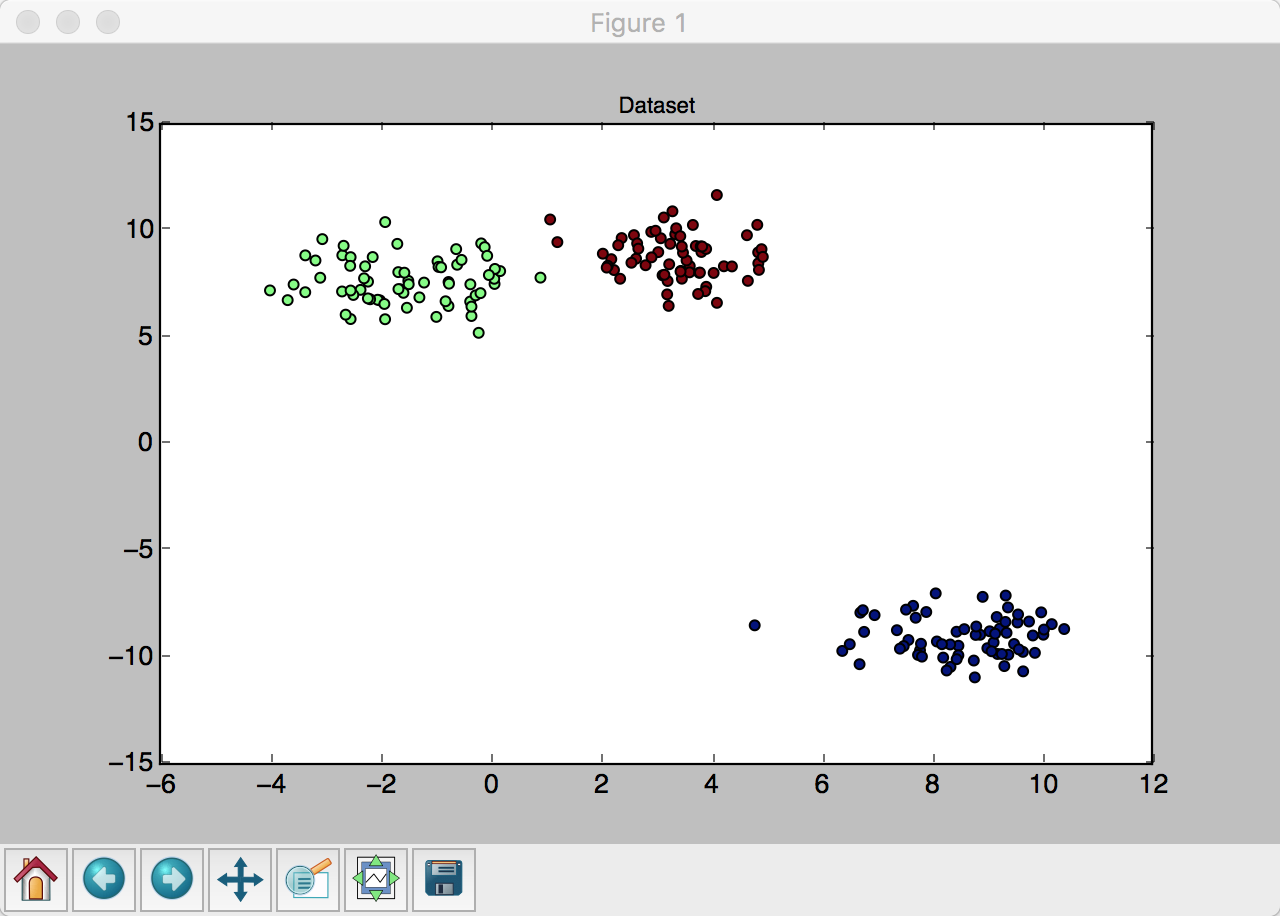
k-means运行后的聚类：

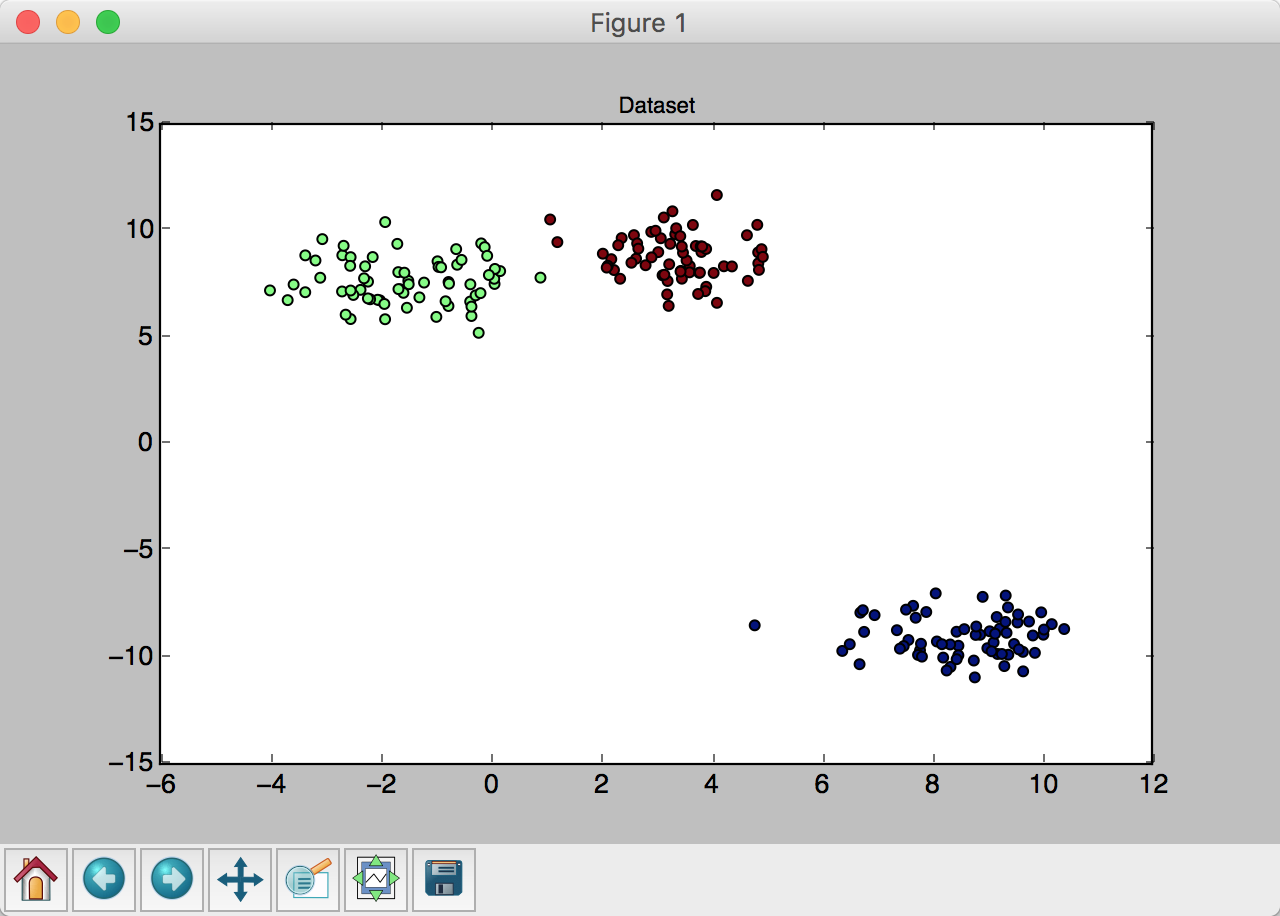
可以看到分类算法运行良好。