机器学习学习笔记(十二)无监督学习K-means
当给出一组未经标记的数据,让程序自己去对其数据结构进行分析与分类(加上标签),就是无监督学习。
例如聚类就是无监督学习中的一个典型例子。
K-means算法
K-means算法(K均值算法)是现在使用最为广泛的聚类算法。
使用步骤如下:
首先随机选择两个点(分成两个聚类),称其为聚类中心;
K-means是一个迭代算法,它将不断进行簇分配与聚类中心移动。
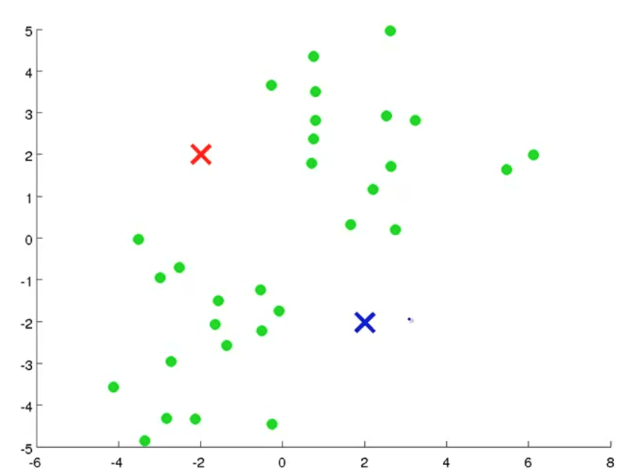
1、簇分配
根据数据集中的点距离哪个聚类中心更近从而将其分为两类,例如:
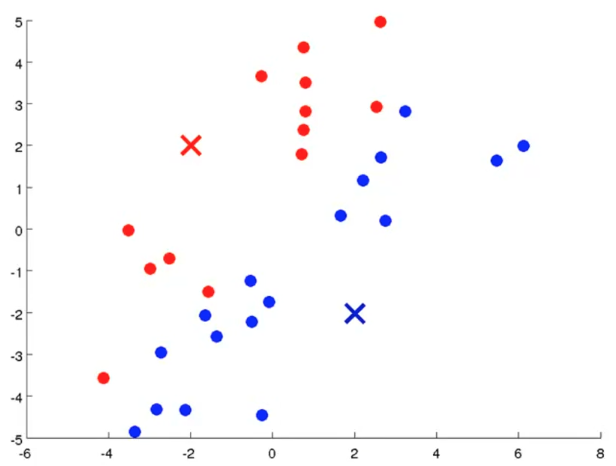
2、移动聚类中心
分别将之前的两个聚类中心移动到它那个聚类的均值处。如图:
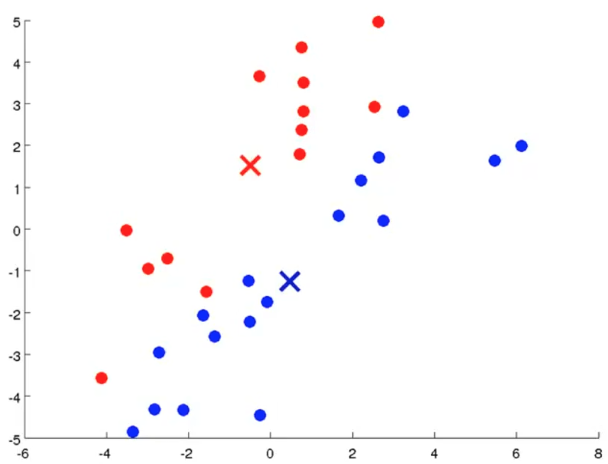
两个中心都移动到均值处。
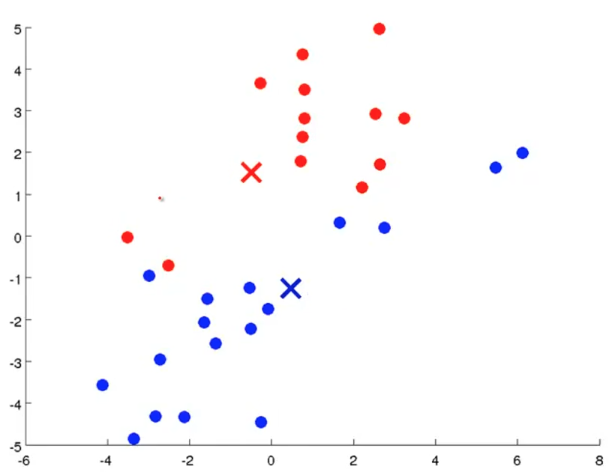
之后再次重复第一步簇分配,重新根据数据点距离聚类中心的距离重新分类,之后再次移动聚类中心……
一直迭代下去,直到聚类中心不再移动,簇分配也不再变化,此时称此时K-means已经收敛了。
以较科学的方式描述K-means

K为簇数,即期望将未标记的数据分为几类的值;
具体算法:

1、随机初始化K个聚类中心Mu1,Mu2……MuK
重复以下的事情:
2、将x中的每个值根据距离Mu的距离分类(簇分配),距离公式如下:
\[min_k \left | x^{(i)}-\mu_k \right |^2\]
3、对于每个聚类中心重新规划在其对应聚类的平均值处。
K-means的实际用途
例如市场细分:
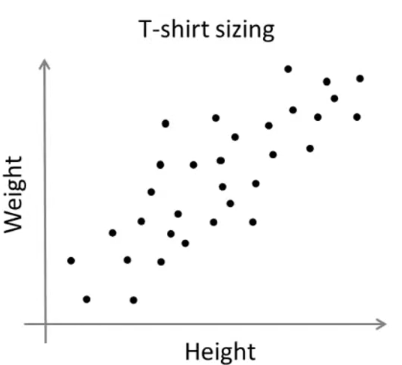
对于服装场来说,如果要将调查到的如上数据的人群分为大中小三个聚类,肉眼从图上看无法分开这三种尺寸。
使用K-means可以将其顺利分为3个聚类,
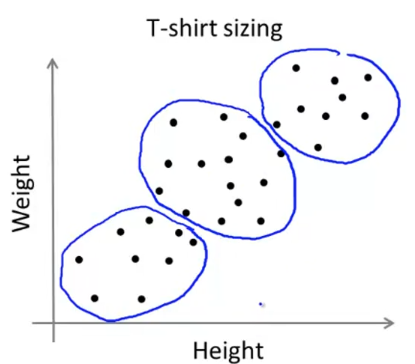
由此可以看到K均值的确可以比人更好的解决一些问题。