机器学习学习笔记(九)过拟合,欠拟合与正则化
过拟合与欠拟合
举例:
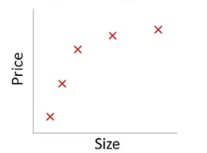
例如对与如上曲线的拟合,如果用两个参数表示,则会成为一条直线,不能正确的表示出size与price间的通常关系。如下图
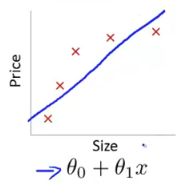
加入一个二次项后,会发现拟合情况变好了,曲线基本能够反映出数据集中各点的位置,并能判断size与price的大概关系。如下图
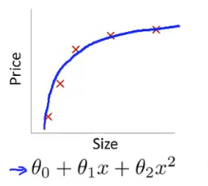
另一个极端情况是,当继续加入多项式时,会发现得到了一条扭曲的曲线,在不断地上下波动。看上去它拟合了所有数据集中的点,但是很明显这不是一个能够真实反应Size与Price的曲线。
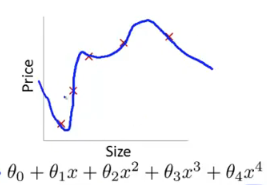
第一种情况由于参数过少,项数过少不能很好拟合数据的情况就是欠拟合;第三种情况由于项数过多,变量太多而没有更多的数据去约束这个过多变量的模型,就会导致过度拟合,或者叫过拟合(overfittin)
逻辑回归中一样有这样的情况,如图
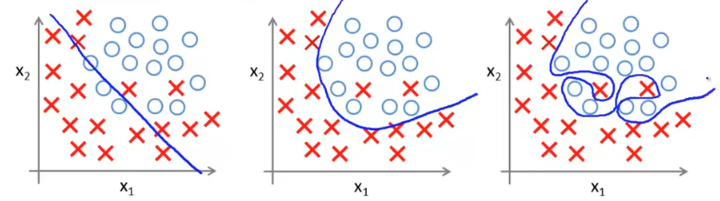
欠拟合的改进比较简单,增加参数增加多次项即可。
过拟合则需要“正则化”来对其进行约束。
正则化
过拟合的一个特征就是高方差。如何避免过拟合的情况呢?可以通过减少变量的形式来避免过拟合。而具体减少哪些变量并不能在所有的模型中很快得出,因此只能说是尽量减少所有的参数值。
\[ \lambda \sum_{j=1}^{n}\theta^{2}_{j}\]
上式可以表述所有的参数大小的总体。lambda被称为“正则化参数”。为了使上式尽量小,可以将其加入代价函数$ J()$中,
\[ J(\theta )=\frac{1}{2m}[\sum^{m}_{i=1}(h_{\theta }(x^{(i)})-y^{(i)})^{2}+\lambda \sum^{n}_{j=1}\theta ^{2}_{j}]\]
当参数过多过大时,后面的正则化项的值就会很大,因而导致\(J(\theta )\)也变大,从而使这个预测方程得到更多的惩罚,使其像参数变量尽量小的地步靠拢。对正则化过程有影响的是lambda,当lambda数值大的时候,函数收到的惩罚更多,会更快地减少参数数值;当lambda为0的时候,函数则不会对参数进行正则化处理。
因此lambda的值与学习率一样,必须适中才能使正则化的过程正常运转。
线性回归中的正则化
当知道代价函数的正则化后,可以来看梯度下降中的正则化

这是正常没有做正则化的梯度下降,没有对参数过多做出任何惩罚。
在式中加上正则化项,使$$尽量往数值小的方面靠拢
\[\theta_j :=\theta_j - \alpha[\frac{1}{m}\sum^m_{i=1}(h_\theta(x^{(i)})-y^{(i)})x^{(i)}_j)+\frac{\lambda}{m}\theta_j]\]
(也可直接由\(J(\theta )\)求偏导得出。) > 由于已经规定了$x_{0}=1 \(,因此\){0}\(不需要加入到正则化进行惩罚,因此上式其实是从\){1}\(开始的。 > > (在matlab中,下标号是从0开始,因此上式在matlab中表现是从\)_{2}$开始)
可经化简得到这么一个式子
\[ \theta_{j} :=\theta_{j}(1-\alpha\frac{\lambda}{m})-\alpha\frac{1}{m}\sum^{m}_{i=1}(h_{\theta}(x^{(i)})-y^{(i)})x_{j}^{(i)}\](从第二项开始)
\[ 1-\alpha \frac{\lambda}{m} \]是小于1的
因此在迭代中,$$会因为参数过大过多被惩罚加速下降,最后以此避免过拟合的出现。
可以推广到逻辑回归的正则化,与线性回归是一样的,只是它们的h(z)和g(x)不一样。
更高级的优化函数中都一样,只是将CostFucion里面加上\(\frac{\lambda }{2m}\sum_{j=1}^{n}\theta^{2}_{j}\)正则化值。
暂不深入正则化的向量写法。