机器学习学习笔记(三)
把一个参数的情形推广到两个参数,每个\(\theta_0\)都对应一组J与\(\theta_1\),表现在坐标图上呈现出一个碗状图形
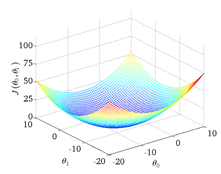 * * *
* * *
用了等高线的概念来理解这个图,可以做出它的“等高图”(轮廓图,contour figure)

横坐标与纵坐标便代表了两个参数,不同的圆弧代表了不同的代价函数值。
发现通过不断地降低J的值,可以得到更好的预测函数的拟合。
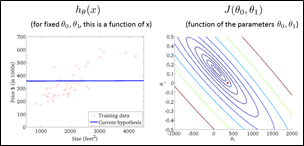
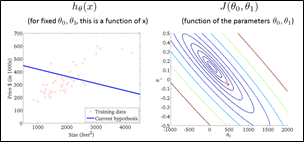
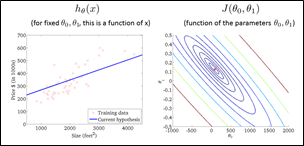 * * *
* * *
梯度下降
为了让J尽可能的小,因此要同时考虑\(\theta_1\)与\(\theta_0\)的值。如果\(\theta_1\)保持不动,\(\theta_0\)就要往得到更小J的方向取值,反之亦然。可以理解成人站在山坡上,一步一步地向地势低的地方走,最终会到达“局部最低点”(local minimum)。
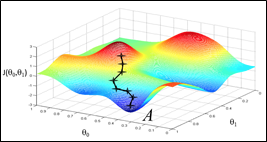
于是可以看到,影响这个过程的有几个因素:起始的位置,每步的步长和每个点的某方向上的斜率。
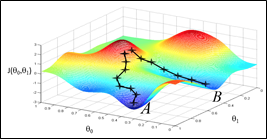
发现不同的起始位置可能会到达不同的局部最小值。因为这种“下山”的方式不是全面的,没有测算两个参数的所有情况。
回到只有一个参数的情况上看。
\(\theta_1:=\theta_1-\alpha\frac{d}{d\theta_1}J(\theta_1)\)( := 符号代表赋值)
\(\theta_1\)连续不断地减去当时的斜率与步长(合适的步长)的乘积,会向局部最小值滑动(可用高数证明),越接近局部最小值斜率就越小,值移动的就越慢,最后无限趋近到达导数为0的点。
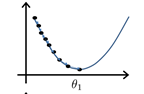
当步长的取值过大时,\(\theta_1\)有可能直接滑过局部最小值而到了极值点的另一侧,此时导数符号反转,与上面的趋近最小值的过程刚好相反,\(\theta_1\)越来越远离这个点。
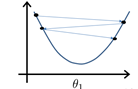
但是当步长取值过小时,找到局部最小值的过程会变得太过漫长,效率低下 by the way,如果起始点一开始就在一个极小值点上时,其导数为0,它不再会发生变化
为了得到收敛值,可列出如下算式。

带入原式得
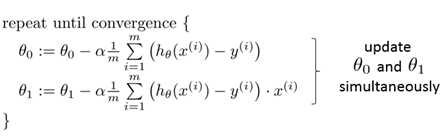
这就是梯度下降算法。
梯度下降算法能得到一个局部最优解,而对于线性回归问题来说,它的坐标图形是碗状的,只有一个最低点,因此用梯度下降法得到的点就是线性回归问题的全局最低值,使J最小,即全局最优解。
梯度下降算法一定是两个参数同时下降才能达到效果