Question Answering over Freebase with Multi-Column Convolutional Neural Networks 论文笔记
《Question Answering over Freebase with Multi-Column Convolutional Neural Networks》发表于 ACL 2015,这篇论文是《Question Answering with Subgraph Embeddings》的后续工作。
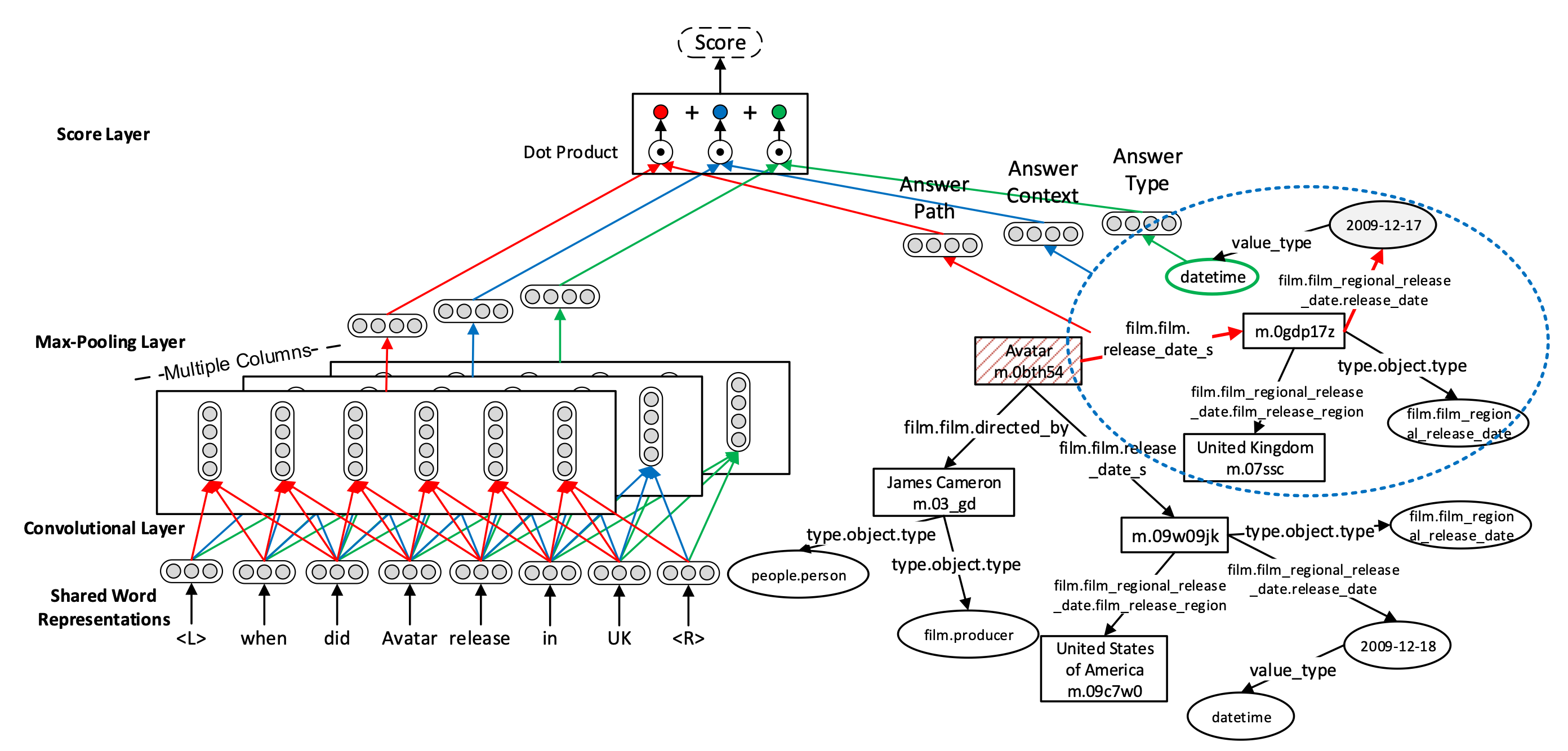
上图展示了该工作的主要模型,可以看到与基于子图嵌入的知识库问答一文类似,也是主要分成了两个部分:问题的文本表示,与答案候选集的子图表示。
对于问题的文本,此论文使用了与TextCNN类似的方式,使用卷积神经网络对问题的词嵌入进行滑动卷积与池化,从而得到问题的文本表示: \[ \mathbf{x}_{j}^{(i)}=\mathbf{h}\left(\mathbf{W}^{(i)}\left[\mathbf{w}_{j-s}^{\top} \ldots \mathbf{w}_{j}^{\top} \ldots \mathbf{w}_{j+s}^{\top}\right]^{\top}+\mathbf{b}^{(i)}\right) \\ \label{chap9:equ:mccnn} \mathbf{f}_{i}(q)=\max _{j=1, \ldots, n}\left\{\mathbf{x}_{j}^{(i)}\right\} \]
其中,\(\mathbf{W}^{(i)}\)是用于获得不同问题表示\(\mathbf{f}_{i}(q)\)的不同的可训练参数矩阵,公式\(\ref{chap9:equ:mccnn}\)表示的是使用滑动窗口进行卷积的具体过程,在此不再赘述。
对于答案候选集,作者设定了三种特征:
(1)答案路径:对于从问题中的实体节点到答案节点的路径的表示,此论文采用了和《基于子图嵌入的知识库问答》中路径表示一样的方法: \[ \mathbf{g}_{1}(a)=\frac{1}{\left\|\mathbf{u}_{p}(a)\right\|_{1}} \mathbf{W}_{p} \mathbf{u}_{p}(a) \]
其中,\(\mathbf{u}_{p}(a)\) 为路径上每一个关系的稀疏向量表示,\(\mathbf{W}_{p}\) 为可训练参数,由于答案路径长度不一,因此作者使用\(\frac{1}{\left\|\mathbf{u}_{p}(a)\right\|_{1}}\)进行了归一化。
(2)答案上下文(Context):该文将与答案相邻一跳的实体和关系称为答案的上下文,使用同样的方法进行嵌入表示: \[ \mathbf{g}_{2}(a)=\frac{1}{\left\|\mathbf{u}_{c}(a)\right\|_{1}} \mathbf{W}_{c} \mathbf{u}_{c}(a) \]
其中,\(\mathbf{u}_{c}(a)\)为答案周围一跳子图的实体和关系的稀疏向量表示,其余参数与答案路径中的相仿。
(3)答案类型:作者认为,类型信息对于知识库问答十分重要,可以根据问题直接限定到答案的类型。例如当问题中有“Where”的时候,答案也应有很大的可能是与“location”相关的类型。因此,作者对答案的类型进行了与前文类似的表示: \[ \mathbf{g}_{3}(a)=\frac{1}{\left\|\mathbf{u}_{t}(a)\right\|_{1}} \mathbf{W}_{t} \mathbf{u}_{t}(a) \]
如果答案是属性值,作者会将答案的类型定义为它的数值类型(如浮点数、字符串、日期等)。
获得上述三种答案候选的特征后,作者将这些特征与问题的表示进行联合打分计算相似度: \[ S(q, a)=\underbrace{\mathbf{f}_{1}(q)^{\top} \mathbf{g}_{1}(a)}_{\text {answer path }}+\underbrace{\mathbf{f}_{2}(q)^{\top} \mathbf{g}_{2}(a)}_{\text {answer context }}+\underbrace{\mathbf{f}_{3}(q)^{\top} \mathbf{g}_{3}(a)}_{\text {answer type }} \]
然后同样使用hinge loss损失函数进行训练: \[ \sum_{q} \frac{1}{\left|A_{q}\right|} \sum_{a \in A_{q}} \sum_{a^{\prime} \in R_{q}} l\left(q, a, a^{\prime}\right) \\ l\left(q, a, a^{\prime}\right)=\left(m-S(q, a)+S\left(q, a^{\prime}\right)\right)_{+} \]
其中\(a^{\prime}\)为答案\(q\)的负样本(即错误答案)。
实验证明,这篇论文的方法比《Question Answering with Subgraph Embeddings》的方法效果更好。作者构建了消融实验,用数据证明了上述的各个特征和步骤都对最终的结果有着正面的影响。