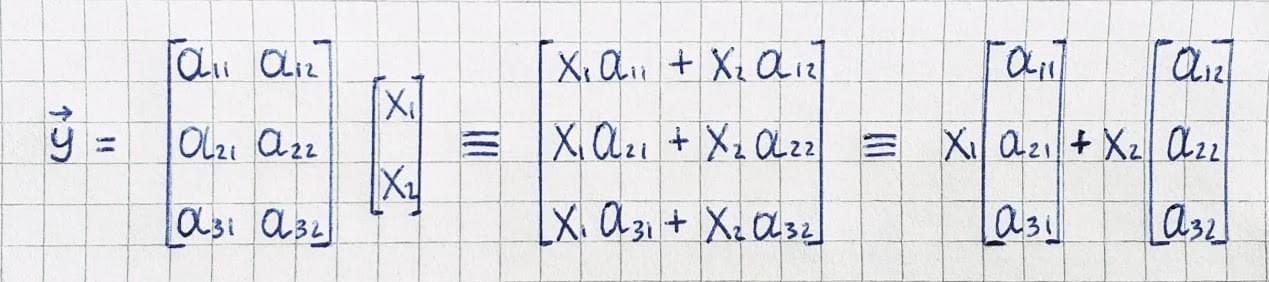本文是“JavaScript
线性代数”教程的一部分。
矩阵是一种由 m 行
n 列实数组成的“矩形”数组。比如,一个
3x2 的矩阵如下所示:
 3×2 矩阵
3×2 矩阵
Matrix
类的构造器(constructor)接收若干行元素作为参数。我们可以通过指定行号取出矩阵中的一行,然后再通过指定列号取出一个特定的元素。下面直接看代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| class Matrix {
constructor(...rows) {
this.rows = rows
}
}
const matrix = new Matrix(
[0, 1],
[2, 3],
[4, 5]
)
console.log(matrix)
console.log(matrix.rows[1])
console.log(matrix.rows[1][1])
|
矩阵与向量的乘积
矩阵与向量的乘法 —— \(A\vec{x}\) 会将矩阵 \(A\) 的列进行系数为 \(\vec{x}\) 的线性组合。比如,一个 \(3\times 2\) 的矩阵 A 与一个
2D 向量 x⃗ 的乘积将得到一个
3D 向量,这个计算记为:\(\vec{y} : \vec{y} = A\vec{x}\)。
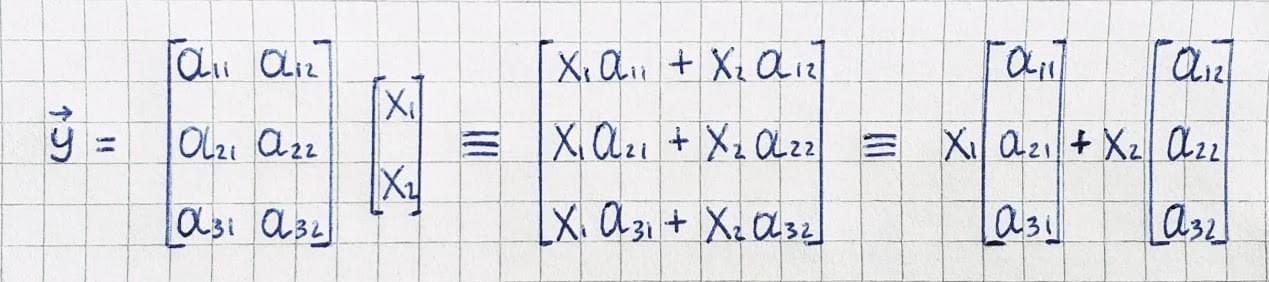
假设有一组向量 \(\{\vec{e}_1,\vec{e}_2\}\),另一个向量 \(\vec{y}\) 是 \(\vec{e}_1\) 和 \(\vec{e}_2\)
的线性组合:\(\vec{y} =
\alpha\vec{e}_1 + \beta \vec{e}_2\)。其中,\(\alpha, \beta \in \mathbb{R}\)
就是这个线性组合的系数。
为了更好地学习线性组合,我们特地为此定义了矩阵向量乘法。我们可以将前面所说的线性组合记为以下矩阵向量乘法的形式:\(\vec{y} = E \vec{x}\)。矩阵 \(E\) 有 \(\vec{e}_1\)、\(\vec{e}_2\) 两列。矩阵的维数是 \(n \times 2\),其中 \(n\) 是向量 \(\vec{e}_1\)、\(\vec{e}_2\) 与 \(\vec{y}\) 的维数。
下图展示了将向量 \(\vec{v}\)
表示为向量 \(\vec{\imath}\) 和向量
\(\vec{\jmath}\) 的线性组合:
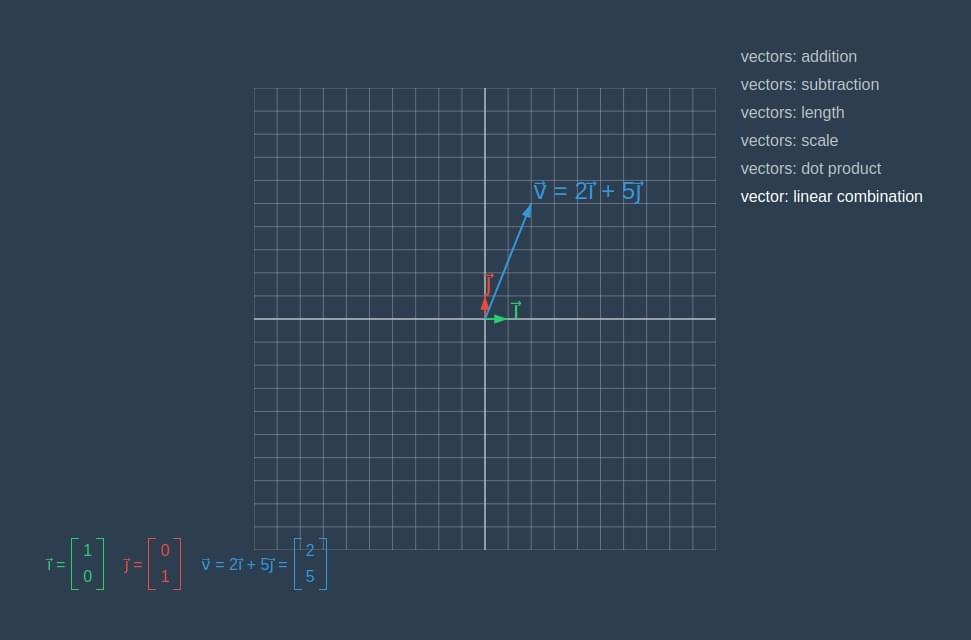 线性组合
线性组合
1
2
3
4
5
6
7
| const i = new Vector(1, 0)
const j = new Vector(0, 1)
const firstCoeff = 2
const secondCoeff = 5
const linearCombination = i.scaleBy(firstCoeff).add(j.scaleBy(secondCoeff))
console.log(linearCombination)
|
线性变换
矩阵与向量的乘法是线性变换的抽象概念,这是学习线性代数中的关键概念之一。向量与矩阵的乘法可以视为对向量进行线性变换:将
n 维向量作为输入,并输出 m
维向量。也可以说,矩阵是定义好的某种空间变换。
我们可以通过一个示例来更清楚地理解线性变换。首先需要给 Matrix
类加上一个方法,用于返回矩阵的列:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| class Matrix {
constructor(...rows) {
this.rows = rows
}
columns() {
return this.rows[0].map((_, i) => this.rows.map(r => r[i]))
}
}
const matrix = new Matrix(
[1, 2, 3],
[4, 5, 6],
[7, 8, 9]
)
console.log(matrix.columns())
|
乘法得到的向量的维数将与矩阵的行数相同。如果我们将一个
2D 向量和一个 3x2 矩阵相乘,将得到一个
3D 的向量;如果将一个 3D 向量和一个
2x3 矩阵相乘,将得到一个 2D
的向量;如果在做乘法时,矩阵的列数和向量的维数不相同,将报错。在下面的代码中,你可以看到几种不同的向量与矩阵相乘的形式:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
| const sum = arr => arr.reduce((acc, value) => acc + value, 0)
class Vector {
transform(matrix) {
const columns = matrix.columns()
if(columns.length !== this.components.length) {
throw new Error('Matrix columns length should be equal to vector components length.')
}
const multiplied = columns
.map((column, i) => column.map(c => c * this.components[i]))
const newComponents = multiplied[0].map((_, i) => sum(multiplied.map(column => column[i])))
return new Vector(...newComponents)
}
}
const vector2D = new Vector(3, 5)
const vector3D = new Vector(3, 5, 2)
const matrix2x2D = new Matrix(
[1, 2],
[3, 4]
)
const matrix2x3D = new Matrix(
[1, 2, 3],
[4, 5, 6]
)
const matrix3x2D = new Matrix(
[1, 2],
[3, 4],
[5, 6]
)
console.log(vector2D.transform(matrix2x2D))
console.log(vector3D.transform(matrix2x3D))
console.log(vector2D.transform(matrix3x2D))
console.log(vector2D.transform(matrix2x3D))
|
示例
现在,我们将尝试对二维的对象应用线性变换。首先,需要创建一个新的
Contour(轮廓)类,它在 constructor
中接收一系列的向量(在 2D 平面中形成一个轮廓),然后用唯一的方法 ——
transform
对轮廓中的所有向量坐标进行变换,最后返回一个新的轮廓。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| class Contour {
constructor(vectors) {
this.vectors = vectors
}
transform(matrix) {
const newVectors = this.vectors.map(v => v.transform(matrix))
return new Contour(newVectors)
}
}
const contour = new Contour([
new Vector(0, 0),
new Vector(0, 4),
new Vector(4, 4),
new Vector(4, 0)
])
|
现在,请在 linear-algebra-demo
项目中试试各种转换矩阵。红色方块是初始化的轮廓,蓝色形状是应用变换矩阵后的轮廓。
 镜像
镜像
 缩放
缩放
通过下面的方式,我们可以构建一个矩阵,用于将给定的向量旋转指定的角度。
1
2
3
4
5
6
| const angle = toRadians(45)
const matrix = new Matrix(
[Math.cos(angle), -Math.sin(angle)],
[Math.sin(angle), Math.cos(angle)]
)
|
 旋转
旋转
 剪切变换
剪切变换
对 3D
空间内的对象进行变换也与此类似。你可以在下图中看到一个红色方块变换成一个蓝色的平行六边形的动画。
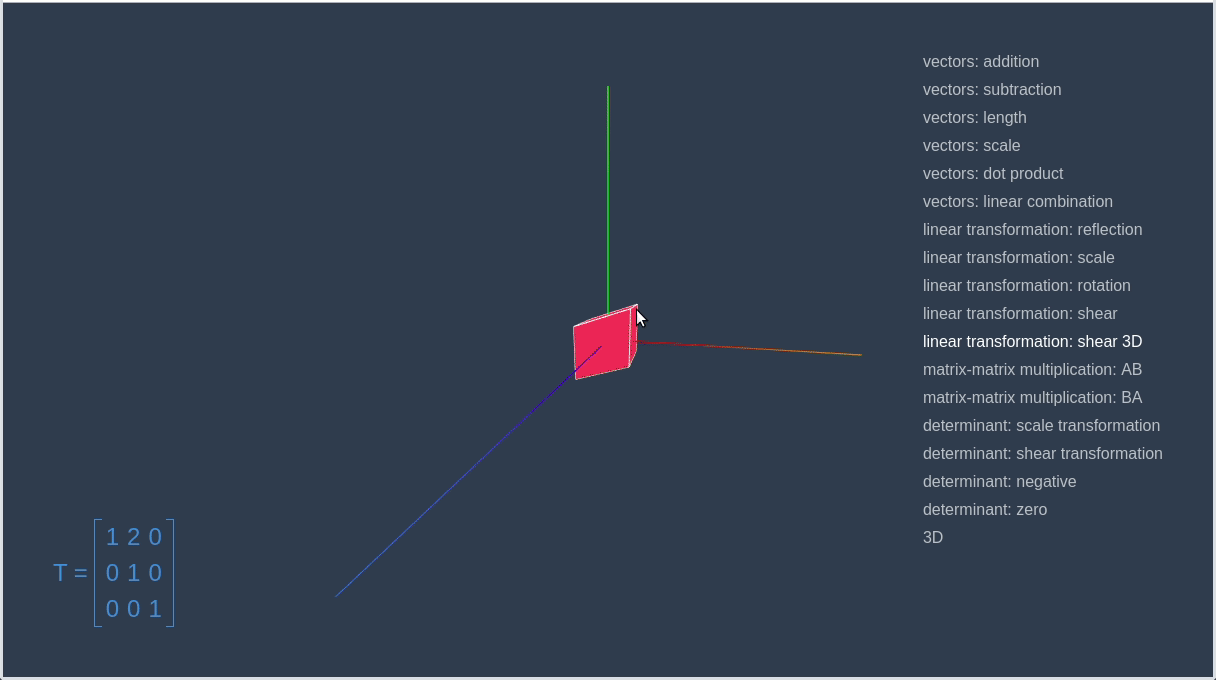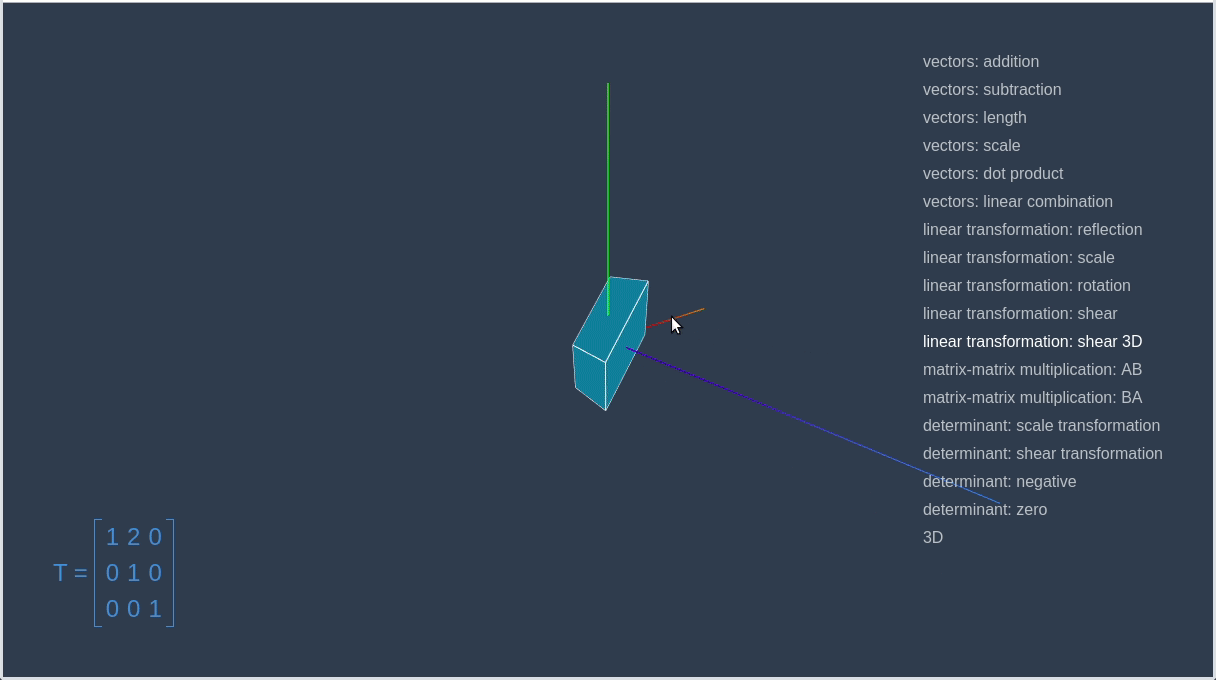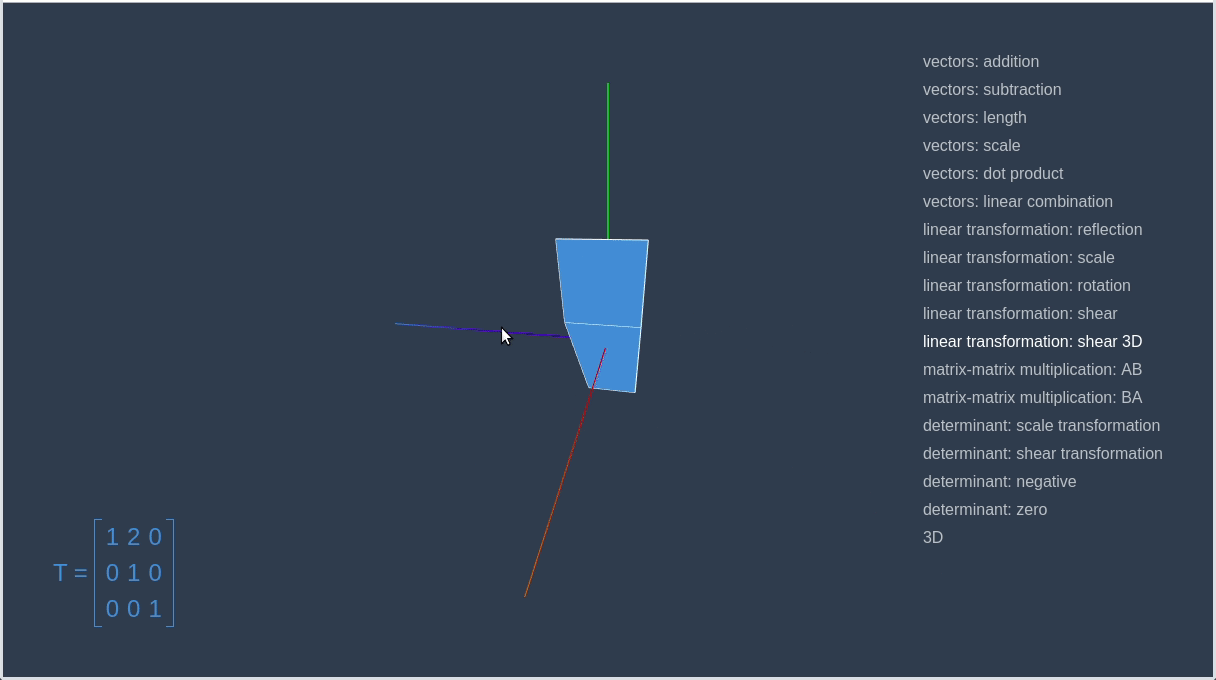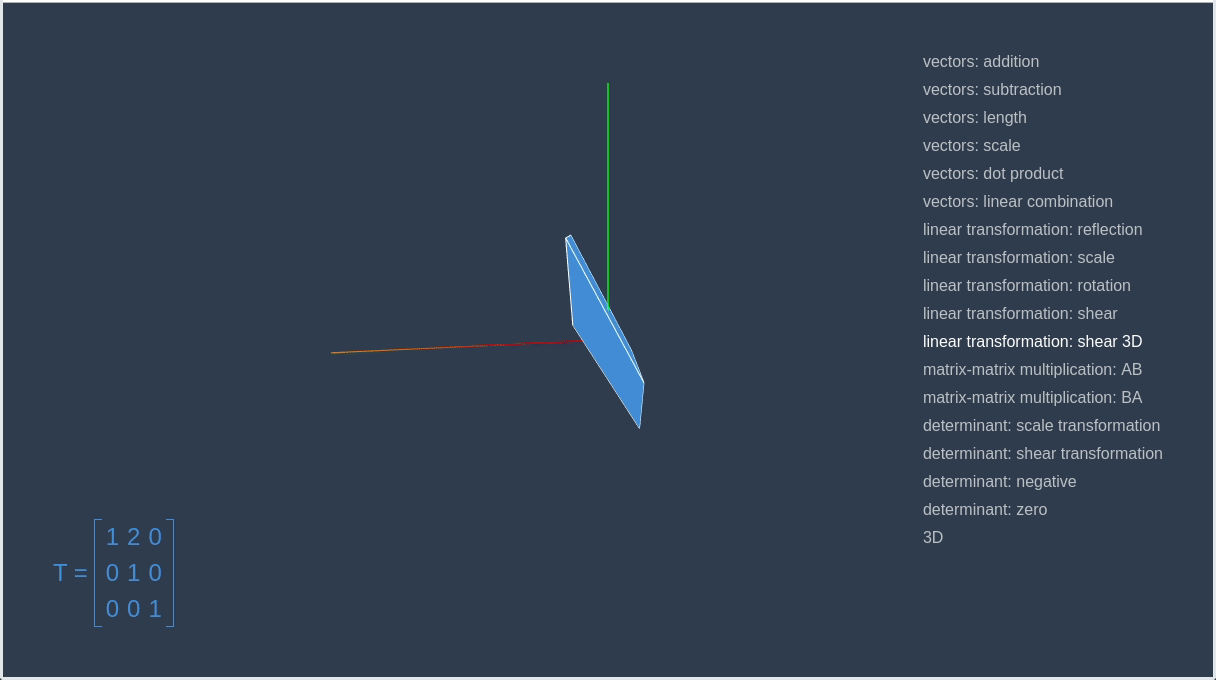 3D 剪切变换
3D 剪切变换