Algorithms for Non-negative Matrix Factorization,非负矩阵分解 论文翻译
NIPS 2000 经典论文 非负矩阵分解算法 翻译
摘要
非负矩阵分解(NMF)是一种可以有效处理多变量数据的方法。本文介绍、分析了两种不同的 NMF 算法,这两种算法仅在更新规则(update rule)中使用的乘性因子(multiplicative factor)有所区别。其中一种可以对传统的最小二乘误差进行最小化(minimize),而另一种可以对广义 Kullback-Leibler 散度(KL 散度)进行最小化。可以使用与证明最大化期望算法收敛性类似的辅助函数来证明这两种算法的单调收敛性。这两种算法均可理解为用斜向最陡下降法(diagonally rescaled gradient descent)对因子进行最优化,以保证算法收敛。
简介
PCA、矢量量化(Vector Quantization)等无监督学习算法可以理解为在不同约束条件下对数据矩阵进行分解。根据其约束的不同,分解所得的因子的会表现出大相径庭的性质。比如,PCA 仅使用了弱正交约束,从而得到非常分散的表示,对这些表示使用消去法来产生多样性;矢量量化使用一种严格的全局最优型约束,最终会得到互斥的数据聚类原型。
我们之前已经证明过,在矩阵分解用于学习数据的部分表示中,非负性(non-negative)是一种非常有用的约束。学习得到的非负基向量是分散的,但仍可通过稀疏的组合,在重建时得到效果良好的表达向量。在本文中,我们详细分析了这两种用于在数据中学习最优的非负因子的数值算法。
非负矩阵分解
下面我们正式开始分析如何用算法解决以下问题:
在非负矩阵分解(NMF)中,给定非负矩阵V,找到非负矩阵因子W和H,使得:
\[(1): V\approx WH \]
NMF 可以应用下面的方法用于对多变量数据进行统计分析。给定一组多变量的 n 维数据向量,其向量位于一个 \(n\times x\) 矩阵 V 的列中(m 表示数据集中的示例数)。然后将此矩阵近似分解为 \(n\times r\) 的 W 矩阵与 \(r\times m\)的 H 矩阵。通常 r 要小于 n 或 m,以使 W 和 H 小于原始矩阵 V。最终得到的是原始数据矩阵的压缩形态。
公式(1)中约等于的意义在于它可以将公式逐列用 \(v\approx Wh\) 来表示,其中 v 和 h 是矩阵 V 和矩阵 H 的对应的列。也就是说,每个数据向量 v 近似地由矩阵 W 的各列线性组合而成,同时用 h 的分量进行加权。因此可以被认为 W 包含了对 V 中的数据的线性近似优化的基向量。由于要使用少量的基向量来表示大量的数据向量,因此只有在基向量发现数据中的潜在结构时才能实现较好的近似。
本文不会涉及关于 NMF 的应用,而会侧重于在技术方面探讨非负矩阵分解的技术。当然,已经有许多其它的矩阵分解方式在数值线性代数中得到了广泛的研究,但是以前的大多数工作都不适用于非负性约束情况。
在此,我们讨论了基于迭代更新 W 和 H 的两种 NMF 算法。由于这两种算法易于实现,同时能保证其收敛性,因此它们在现实情况中非常实用。其他算法可能在总计算时间方面更有效率,但是更难实现,并且很难推广到不同的代价函数(cost function)。因子与我们类似的算法,已经被用于对发射断层扫描和天文图像进行反卷积(deconvolution)。
在我们算法的每次迭代中,会用当前值乘某些取决于公式(1)中的“近似程度”的因数,来找到 W 或 H 的新值。我们可以证明“近似程度”会随着不断应用这些乘法更新规则而单调减小。这正意味着更新规则的重复迭代可以保证矩阵分解算法收敛到局部最优。
代价函数
为了找到$ VWH $的近似解,我们首先需要定义一个代价函数,用以量化近似的程度。可以使用两个非负矩阵 A 和 B 的距离来构造此代价函数。一种使用的距离度量方法为:计算 A 和 B 之间的欧几里得距离(Euclidean distance)的平方值。
\[(2): ||A-B||^2 = \sum_{ij}(A_{ij} - B_{ij})^2 \]
此公式下界为 0,仅当 A=B 时距离消失。
另一种实用的度量方式为:
\[(3): D(A||B) = \sum_{ij}(A_{ij} \log{\frac{A_{ij}}{B_{ij}}} - A_{ij}+B_{ij})\]
与欧几里得距离相同,它的下界也为 0,且在 A=B 时距离消失。但它不能被称为“距离”,因为这个式子在 A 与 B 中并不对称,因此我们将其称为 A 对于 B 的“散度”(divergence)。它可以归纳为 KL 散度或者相对熵,当 \(\sum_{ij}A_{ij}=\sum_{ij}B_{ij}=1\) 时,A 与 B 可以看做是标准化的概率分布。
现在,我们可以按照以下两种公式来将 NMF 化为最优化问题:
最优化问题1:在约束条件 \(W, H \geq 0\) 下,以 W 和 H 作为参数,最小化 \(||V - WH||^2\)。
最优化问题2:在约束条件 \(W, H \geq 0\) 下,以 W 和 H 作为参数,最小化 \(D(V||WH)\)。
虽然方程 \(||V - WH||^2\) 和 \(D(V||WH)\) 在只考虑 W 或 H 之一时为凸,但在同时考虑 WH 两个变量时不为凸。因此,寻找一种可以找到全局最小值的算法去解决以上两个最优化问题是不切实际的。但是,还有许多数值优化方法可以用于寻找局部最小值。
虽然梯度下降法(Gradient descent)的收敛速度很慢,但它的实现最为简单。其它方法(比如共轭梯度法)可以更快地收敛(至少在局部最小值附近会更快),但是它们比梯度下降更复杂。此外,梯度下降方法的收敛对步长的选择非常敏感,这对于大规模应用十分不利。
乘法更新规则
我们发现在解决上述两个最优化问题时,在速度与实现难度中权衡,“乘法更新规则”是一种综合性能很好方法。
定理1:欧几里得距离 \(||V-WH||\) 在下面的更新规则中呈非增:
\[(4): H_{a\mu} \leftarrow H_{a\mu}\frac{(W^T V)_{a\mu}}{(W^T W H)_{a\mu}}\]
\[(4): W_{ia} \leftarrow W_{ia}\frac{(V H^T)_{ia}}{(W H H^T)_{ia}}\]
在上述更新规则中,W 与 H 在距离公式的驻点上时,欧几里得距离将固定不动。
定理2:散度 \(D(V|WH)\) 在下面的更新规则中呈非增:
\[(5): H_{a\mu} \leftarrow H_{a\mu}\frac{\frac{\sum_{i}W_{ia}V_{i\mu}}{WH_{i\mu}}}{\sum_k W_{ka}}\]
\[(5): W_{ia} \leftarrow W_{ia}\frac{\frac{\sum_{\mu}H_{a\mu}V_{i\mu}}{WH_{i\mu}}}{\sum_v H_{av}}\]
在上述更新规则中,W 和 H 在散度公式的驻点上时,散度将不再更新。
上述定理的证明将在后面给出。我们可以发现,每次更新都是乘以一个因子。特别地,当V = WH时,可以直观地看出这个乘数因子是一样的,当更新规则固定时,才会得到完美的分解。
乘法与加法更新规则
可以将乘法更新与梯度下降更新进行对比。特别的,对 H 进行更新以减小平方距离可以记为:
\[ (6):H_{a\mu} \leftarrow H_{a\mu} + \eta_{a\mu}[(W^TV)_{a\mu} - (W^T WH)_{a\mu}] \]
如果将 \(\eta_{a\mu}\) 设置为较小的正数,上式就和常规的梯度下降等价。只要数字充分小,就能在更新时减小 \(||V-WH||\)。
如果我们按照斜向最陡调整变量,并设置:
\[ (7): \eta_{a\mu}=\frac{H_{a\mu}}{(W^TWH)_{a\mu}}\]
就能得到定理 1 中给出的 H 更新规则。注意,该调整可得出乘性因子(分母中的梯度的正分量和因子的分子中的负分量的绝对值)。
对于散度公式,我们按照下述公式调整斜向最陡梯度下降:
\[ (8): H_{a\mu} \leftarrow H_{a\mu} + \eta_{a\mu}[\sum_{i}W_{ia}\frac{V_{i\mu}}{(WH)_{i\mu}}-\sum_{i}W_{ia}]\]
同样的,如果将 \(\eta_{a\mu}\) 设置为较小的正数,上式就和常规的梯度下降等价。只要数字充分小,就能在更新时减小 \(D(V||WH)\)。如果设置:
\[ (9): \eta_{a\mu} = \frac{H_{a\mu}}{\sum_i W_{ia}}\]
那么就能得到定理 2 中给出的 H 更新规则。该调整可得出乘性因子(分母中的梯度的正分量和因子的分子中的负分量的绝对值)。
由于我们对 \(\eta_{a\mu}\) 的取值并不够小,看起来不能保证这种调整过后的梯度下降的代价函数减小。不过让人惊讶的是,如下节所示,上述假设是事实。
收敛证明
我们将使用一个类似于 EM 算法的辅助函数来证明定理 1 与定理 2。
定义 1:\(G(h,h')\) 是 \(F(h)\) 的辅助函数,满足以下条件成立:
\[(10): G(h,h')\geq F(h), G(h,h)=F(h) \]
根据下面的引理,此辅助函数是一个有用的概念。(在图1中的插图也显示了这一点)
引理 1:如果 G 为辅助函数,则 F 在下述更新时为非增:
\[(11): h^{t+1} = \arg\min_{h}G(h,h^t)\]
证明:\(F(h^{t+1}) \leq G(h^{t+1}, h^t) \leq G(h^t,h^t) = F(h^t)\)
请注意,只有在\(h^t\)为\(G(h,h^t)\)的全局最小值时满足\(F(h^{t+1})=F(h^t)\)。如果 F 的导数存在,且在\(h^{t}\)的邻域连续,也就是说$F(h^t) = 0 $。因此通过公式11反复更新,我们就能得到目标函数收敛的局部最小值 \(h_{min} = \arg\min_h F(h)\)
\[(12): F(h_{min}) \leq ... F(h^{t+1})\leq F(h^t) ... \leq F(h_2) \leq F(h_1) \leq F(h_0)\]
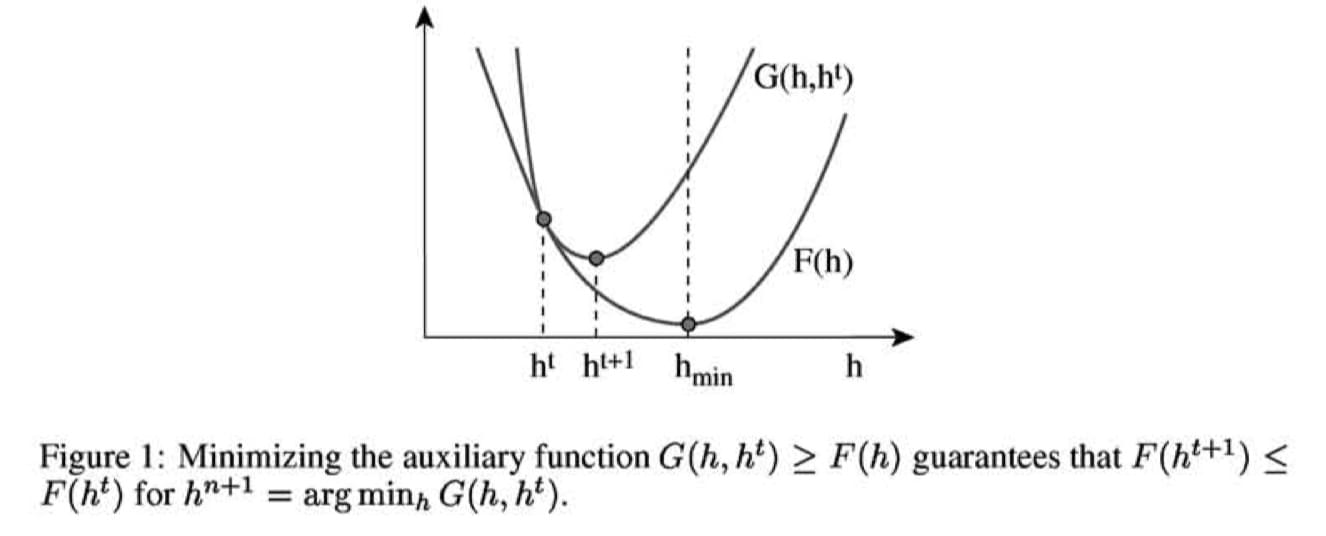
下面,我们证明如何为\(||V-WH||\)与\(D(V,WH)\)定义适当的辅助函数\(G(h,h^t)\)。定理 1 与定理 2 可以直接遵循公式 11 的更新规则。
引理 2:如果\(K(h^t)\)为对角矩阵,
\[(13): K_{ab}(h^t) = \delta_{ab}\frac{W^T Wh^t}{h^t_a}\]
则
\[(14): G(h,h^t)=F(h^t)+(h-h^t)^T \nabla F(h^t) + \frac{1}{2}(h-h^t)^T K(h^t)(h-h^t)\]
为
\[(15): F(h)=\frac{1}{2} \sum_i(v_i- \sum_a W_{ia} h_a)^2\]
的辅助函数。
证明:因为显然 \(G(h,h)=F(h)\),因此只需证明 \(G(h,h') \geq F(h)\)。为了证明此不等式,需要将
\[(16): F(h) = F(h^t) + (h-h^t)^T \nabla F(h^t) + \frac{1}{2}(h-h^t)^T(W^TW)(h-h^t)\]
与公式 14 进行对比,发现 \(G(h,h') \geq F(h)\) 等价于
\[(17): 0 \leq (h-h^t)^T[K(h^t) - W^TW](h-h^t)\]
为证明半正定情况,考虑矩阵:
\[(18): M_{ab}(h^t)=h_a^t(K(h^t)-W^TW)_{ab}h_b^t\]
仅是\(K-W^TW\)的调整形式。因此,仅当 M 符合下列公式时,\(K-W^TW\)具有半正定性:
\[(19):v^T Mv = \sum_{ab}v_a M_{ab} v_b \\ (20):=\sum_{ab}h^t_a(W^TW)_{ab}h^t_bv_a^2-v_ah^t_a(W^TW)_{ab}h_b^tv_b \\ (21):=\sum_{ab}(W^TW)_{ab}h_a^th_b^t[\frac{1}{2}v_a^2 + \frac{1}{2}v_b^2 - v_av_b] \\ (22):=\frac{1}{2}\sum_{ab}(W^TW)_{ab}h_a^th_b^t(v_a-v_b)^2 \\ (23):\geq 0\]
现在,我们可以证明定理 1 的收敛性。
定理 1 证明:使用公式14的结果替换公式11中的\(G(h,h^t)\),得到更新规则:
\[(24): h^{t+1}=h^t - K(h^t)^{-1} \nabla F(h^t)\]
因为公式14为辅助函数,根据引理1,F 在更新规则中为非增。将上式完整的写下来,可以得到:
\[(25): h^{t+1}_a= h^{t}_a \frac{(W^Tv)_a}{(W^TWh^t)_a}\]
反转引理 1 与引理 2 中 W 和 H 的角色,F 可以以类似的方法证明在 W 的更新规则下为非增。
接下来,我们为散度代价方程寻找辅助函数。
引理 3:定义
\[(26): G(h,h^t)=\sum_i(v_i \log{v_i} - v_i) + \sum_{ia} W_{ia}h_a \\ (27):-\sum_{ia}v_i\frac{W_{ia}h^t_a}{\sum_b W_{ib} h^t_b} (\log{W_{ia} h_a - \log{\frac{W_{ia}h^t_a}{\sum_b W_{ib} h^t_b}}})\]
为
\[(28): F(h)=\sum_i v_i \log(\frac{v_i}{\sum_a W_{ia} h_a})- v_i + \sum_a W_{ia} h_a \]
的辅助函数。
证明:因为显然 \(G(h,h)=F(h)\),因此只需证明 \(G(h,h') \geq F(h)\)。我们通过对数函数的凸性来推导此不等式:
\[(29): -\log \sum_a W_{ia} h_a \leq -\sum_a a_a \log \frac{ W_{ia} h_a}{a_a} \]
上式对所有的联合求合数 \(a_a\) 均成立。设
\[(30): a_a =\frac{ W_{ia} h_a}{\sum_b W_{ib} h_b} \]
可以得到:
\[(31): -\log \sum_a W_{ia} h_a \leq - \sum_a \frac{ W_{ia} h_a}{\sum_b W_{ib} h_b} (\log W_{ia} h_a - \log\frac{ W_{ia} h_a}{\sum_b W_{ib} h_b} ) \]
上面的不等式遵循 \(G(h,h') \geq F(h)\)。
定理 2 的证明遵循引理 1 及其应用:
定理 2 证明:要令 \(G(h,h^t)\) 最小化,则需要将梯度设为 0 来求出 h:
\[(32): \frac{dG(h,h^t)}{dh_a} = - \sum_i v_i \frac{ W_{ia} h_a^t}{\sum_b W_{ib} h_b^t} \frac{1}{h_a} + \sum_i W_{ia} = 0\]
因此,公式 11 采取的更新规则应当如下所示:
\[ (33): h_a^{t+1} = \frac{h_a^t}{\sum_b W_{kb}} \sum_i \frac{v_i}{\sum_b W_{ib}h_b^t} W_{ia} \]
因为 G 为辅助函数,公式 28 中的 F 在更新规则中为非增。用矩阵形式重写上述公式,发现与 公式 5 的更新规则等价。反转 W 和 H 的角色,可以以类似的方法证明 F 在 W 的更新规则下为非增。
讨论
我们已经证明了在公式 4 与公式 5 中应用更新规则,可以找到问题 1 与问题 2 的局部最优解。借助定义合适的辅助函数证明了函数的收敛性。我们将把这些证明推广到更复杂的约束条件下去。更新规则在计算上非常容易实现,有望进行广泛的应用。
感谢贝尔实验室的支持,以及 Carlos Brody, Ken Clarkson, Corinna Cortes, Roland Freund, Linda Kaufman, Yann Le Cun, Sam Roweis, Larry Saul, Margaret Wright 的帮助与讨论。