EM algorithm in python

Posted on 2017-03-23 In Algorithm

由之前的学习笔记使用python实现EM算法。

EM algorithm

\[\text{Repeat until convergence}\{\\ \text{(E-step) For each i,set}\\ Q_i(z^{(i)}):=p(x^{(i)},z^{(i)};\theta)\\ \text{(M-step) set}\\ \theta:=\arg \max_\theta \sum^m_{i=1} \sum_{z^{(i)}} Q_i(z^{(i)}) \ln \frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}\}\]

准备数据

和上一篇k-means一样，从准备数据开始。EM算法可以用来对数据集中数据的分布参数进行极大似然估计。因此，为它准备两组一维高斯分布数据。

使用numpy的randn函数来生成正态分布数据，使用matplotlib来对其进行可视化。

1 2	import numpy as np import matplotlib.pyplot as plt

参考numpy的文档，生成一个[latex]N(mu,sigma^2)[/latex]的正态分布，需要使用

mu + sigma * np.random.randn(..)

代码：

def generateDataAndShow():
    x1,x2 = mu1 + sigma * np.random.randn(500),mu2 + sigma * np.random.randn(500)
    x = np.append(x1,x2)
    plt.hist(x,50,normed=True)
    plt.show()
    return x

if __name__=='__main__':
    data = generateDataAndShow()

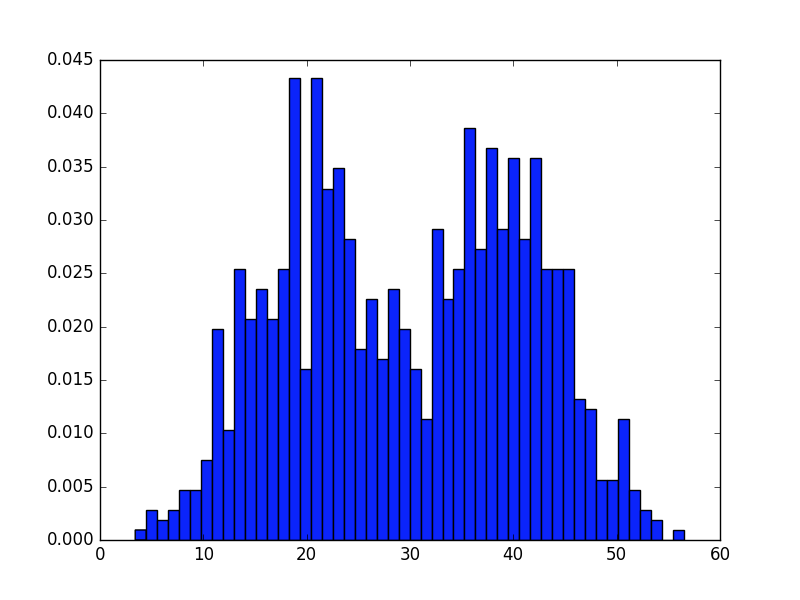
这样，就得到了两组分别以[latex]N(mu_1,sigma^{2)[/latex]与[latex]N(mu_2,sigma}2)[/latex]分布的数据集。通过matplotlib可以看到它们的分布概率图大致如下：

算法实现

算法的推导与分析在http://lsvih.com/?p=515 进行过了。总体来说是一个迭代渐进的过程。渐进的变量有两个，一个是实现分类的隐藏变量z，另一个是决定分布函数的参数[latex]theta[/latex]。

E-step

已知高斯函数的概率密度函数(PDF)为

\[f(x,\sigma,\mu)=\frac{1}{\sigma \sqrt{2\pi}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}\]

for i,X in enumerate(data):
    p1 = np.exp(-(X-mu1)**2/(2*sigma**2))/(sigma*(np.sqrt(2*np.pi)))
    p2 = np.exp(-(X-mu2)**2/(2*sigma**2))/(sigma*(np.sqrt(2*np.pi)))
    Z[i,0],Z[i,1] = p1/(p1+p2),p2/(p1+p2)

即实现\(Q_i(z^{(i)}):=p(x^{(i)},z^{(i)};\theta)\)

M-step

data为矩阵

\[\begin{bmatrix}x_1\\x_2\\...\\x_n\end{bmatrix}\]

而Z为矩阵

\[\begin{bmatrix}Z^{(1)}_1&Z^{(1)}_2\\Z^{(2)}_1&Z^{(2)}_2\\...\\Z^{(n)}_1&Z^{(n)}_2\end{bmatrix}\]

因此完成\(\theta:=\arg \max_\theta \sum^m_{i=1} \sum_{z^{(i)}} Q_i(z^{(i)}) \ln \frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}\)运算可以使用矩阵的点乘实现。

1	mu1,mu2 = np.dot(np.array(data),np.array(Z))/np.sum(Z,axis=0)

Result

在对于E-step与M-step不停的迭代优化后，达到一个期望精度值停止运算。因此main()可以写成

while True:
    o_mu1,o_mu2 = mu1,mu2
    Z = np.zeros([len(data),2])
    #E-Step
    #M-Step
    if abs(o_mu1-mu1)+abs(o_mu2-mu2) <= 0.001:
        print mu1,mu2
        break

在迭代至指定精度后，将得到的mu1与mu2与sigma决定的正态分步曲线画出来。

#Darw Gaussian function
import matplotlib.mlab as mlab
fig, ax = plt.subplots()
n,bins,p = ax.hist(data,50,normed=True)
y1,y2 = mlab.normpdf(bins, mu1, sigma), mlab.normpdf(bins, mu2, sigma)
ax.plot(bins, y1/2)
ax.plot(bins, y2/2)
plt.show()

可以看到，最初的generateData函数中画出的图形为

得到结果后画出的曲线为

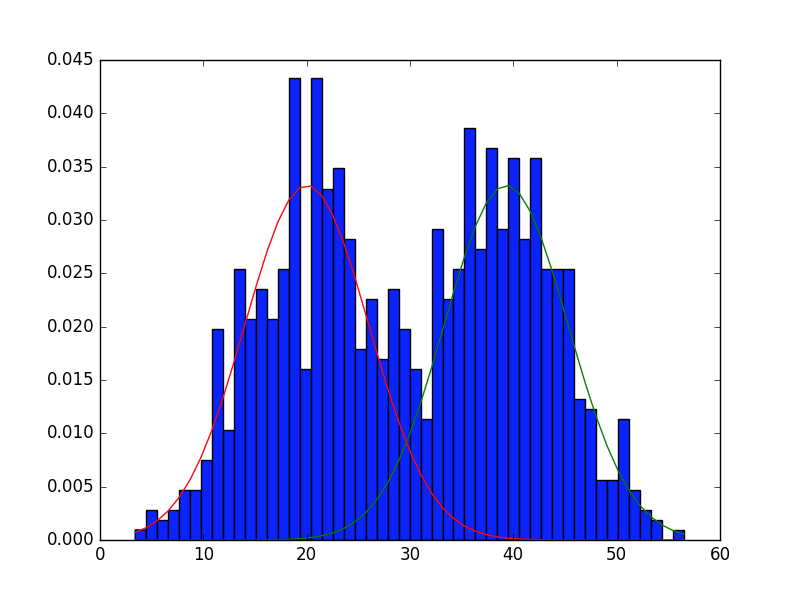
基本能匹配之前生成的数据。