探究函数矩阵化运算——逐步分析对于线性回归代价函数的矩阵化

Posted on 2016-04-21 In Algorithm

在此之前没有接触过矩阵化运算，因此对于矩阵化运算的过程一头雾水。准备对于线性回归的代价函数进行矩阵化以探究其过程。

CostFuction 数学表达式：

\[J(\theta)=\frac{1}{2m}\sum^m_{i=1}(h_\theta(x^{(i)})-y^{(i)})^2\]

根据数学式之前以for循环写了算法：

for i=1:m
J += (theta(1)+ theta(2)*X(i,2)-y(i))^2;
end
J = J/(2*m);

很明确的循环符合数学式。

尝试对齐进行矩阵化，首先看\(h_\theta(x^{(i)})\)

\[h_\theta(x)=\theta^T x = \theta_0 + \theta_1 x_1\]

对每个x(i)进行运算：

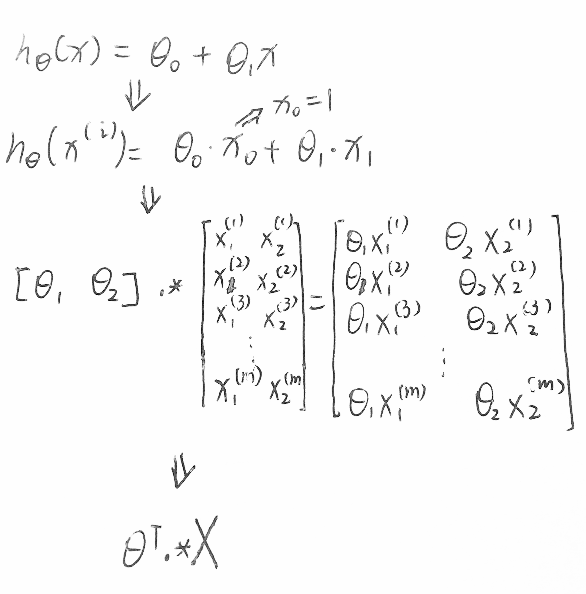
对其进行sum与转置操作后可以得到

\[\sum((\theta'.*X)')-y'= \\ [\theta_1 x^{(1)}_1+\theta_2 x^{(1)}_2 -y^{(1)},\theta_1 x^{(2)}_1+\theta_2 x^{(2)}_2 -y^{(2)},...,\theta_1 x^{(m)}_1+\theta_2 x^{(m)}_2 -y^{(m)}]\]

因此可以得知代价函数的矩阵化函数式为：

1	J = sum((sum((theta'.X)')-y').^2)/(2m);