机器学习学习笔记(十)神经网络前向传播
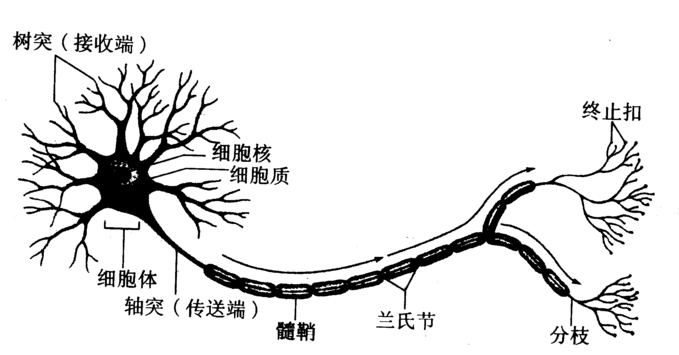
如同人的神经元一般,由输入端-神经元-输出这样一系列过程的信息处理方式,可以处理较为复杂的信息,并有一定的学习功能。
神经网络一般分为:输入层、隐藏层、输出层。对于用户来说,只有输出层的输出是可知的,隐藏层可以完成许多间接的复杂运算,因此神经网络的计算复杂度比单层结构复杂的多。
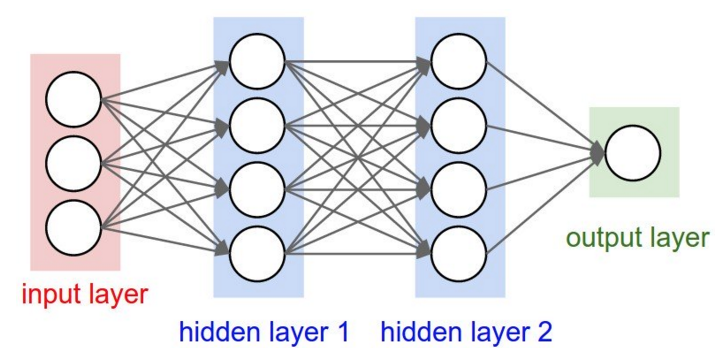
上图为一个有两层隐藏层的典型的神经网络,可以看到其基本结构.可以发现任何一个节点相当于收到上一层所有节点的影响.每个节点影响的程度可以以权值表示。
以下面一个简单的神经网络举例,
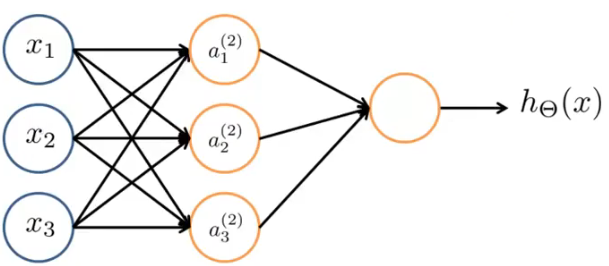
隐藏层(a(2)1,a(2)2,a(2)3)的值的计算为:
\[a^{(2)}_1 = g(\theta ^{(1)}_{10}x_0 + \theta ^{(1)}_{11}x_1 + \theta ^{(1)}_{12}x_2 + \theta ^{(1)}_{13}x_3)\]
\[a^{(2)}_2 = g(\theta ^{(1)}_{20}x_0 + \theta ^{(1)}_{21}x_1 + \theta ^{(1)}_{22}x_2 + \theta ^{(1)}_{23}x_3)\]
\[a^{(2)}_3 = g(\theta ^{(1)}_{30}x_0 + \theta ^{(1)}_{31}x_1 + \theta ^{(1)}_{32}x_2 + \theta ^{(1)}_{33}x_3)\]
\(\theta\)即表示相应层元素受到上一层“激励”的权值。(x0为加上的额外的偏度单元)
g为S函数(解决逻辑回归问题)
同理,输出层的值为
\[h_\theta(x)=a^{(3)}_1 = g(\theta ^{(2)}_{10}a_0 + \theta ^{(2)}_{11}a_1 + \theta ^{(2)}_{12}a_2 + \theta ^{(2)}_{13}a_3)\]
为前一层(隐藏层)的所以元素乘对应的权值的和的对应函数值。
\[a^{(2)}_1 = g(\theta ^{(1)}_{10}x_0 + \theta ^{(1)}_{11}x_1 + \theta ^{(1)}_{12}x_2 + \theta ^{(1)}_{13}x_3)\]
\[a^{(2)}_2 = g(\theta ^{(1)}_{20}x_0 + \theta ^{(1)}_{21}x_1 + \theta ^{(1)}_{22}x_2 + \theta ^{(1)}_{23}x_3)\]
\[a^{(2)}_3 = g(\theta ^{(1)}_{30}x_0 + \theta ^{(1)}_{31}x_1 + \theta ^{(1)}_{32}x_2 + \theta ^{(1)}_{33}x_3)\]
对于以上式子可以看成矩阵相乘的形式,
\[x=\begin{bmatrix}x_0\ x_1\ x_2\ x_3\end{bmatrix}\]
\[z^{(2)}=\begin{bmatrix}z_1^{(2)}\ z_2^{(2)}\ z_3^{(2)}\end{bmatrix}\]
\[z^{(2)} = \theta^{(1)}x\]
\[a^{(2)}=g(z^{(2)})\]
z(2)为第二层元素值的向量形式。(1)为输入层对应的权值的向量形式。
\[z^{(3)} = \theta^{(2)}a^{(2)}\]
\[h_\theta(x)=a^{(3)}=g(z^{(3)})\]
(2)为隐藏层对应权值的向量形式。
神经网络中这种由训练输入送入网络中,获得激励响应的行为称为“前向传播”
神经网络解决实际问题
例如下表:
| x1 | x2 | y |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
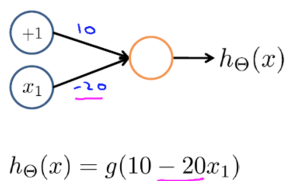
在神经网络中,可以以下形式表示
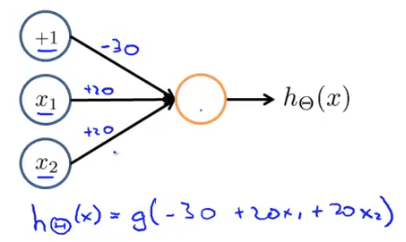
计算一下,发现x1与x2等于0时z=-30,x1与x2等于1时z=10,x1与x2不相等时z=-10.
将其放到S函数中,
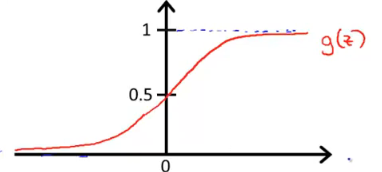
z=-30与z=-10时g(z)趋近与0,z=10时趋近与1,可以表示上表的值的关系。
可以用y=x1 AND x2 (与)表示这个关系。
下表用神经网络表示:
| x1 | x2 | y |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
这种“异或”问题可以看成一个“与”与一个“或”问题的结合,
(NOT)
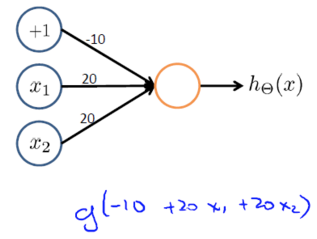
(AND)
(NOT x1)AND(NOT x2)
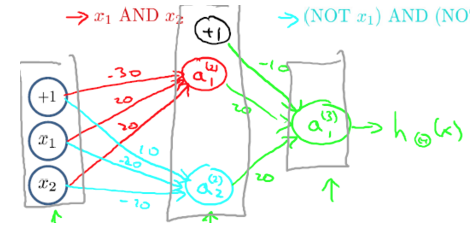
可以得到上表内容。
以上为神经网络表示“异或”运算。
必须要两层网络才能解决异或运算问题。因为1层网络放在坐标图上可以看成是画了一条直线,而异或问题放在图上是这样的:
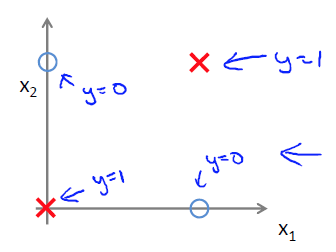
不难发现没有一条直线能够完美地分开两类点。