机器学习学习笔记（八）分类问题实操

Posted on 2016-03-30 In Machine Learning

直线分类问题

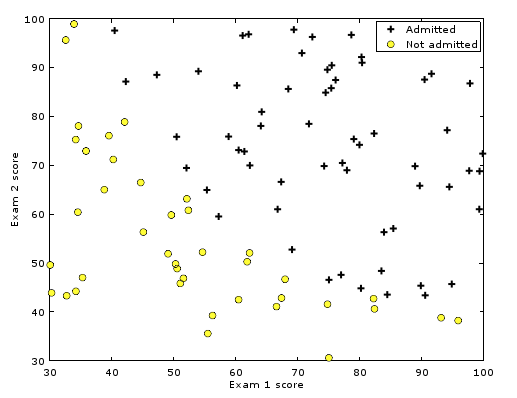
对于此数据图可以发现正类与负类的决策边界大约是一条直线。

与线性回归类似，先计算代价方程J

\[J(\theta_0,\theta_1)=\frac{1}{2m} \sum^m_{i=1}(h_\theta(x^{(i)}-y^{(i)}))^2\]

但是其中的h(x)发生了变化，实际上为

\[h_\theta(x)=g(\theta^Tx)\] \[g(z)=\frac{1}{1+e^{-z}}\]

带入得

\[J(\theta)=\frac{1}{m}\sum^m_{i=1}Cost(h_\theta(x^{(i)},y^{(i)})) \\=-\frac{1}{m}[\sum^m_{i=1}y^{(i)}log{h_\theta(x^{(i)})}+(1-y^{(i)})log{(1-h_\theta(x^{(i)})})]\]

同理带入梯度下降函数

\[\theta:=\theta-\alpha\frac{1}{m}\sum^m_{i=1}[(h_\theta(x^{(i)})-y^{(i)})\cdot x^{(i)}]\]

最后将它们放入fminunc（matlab求最小值函数）中运算即可得到训练结果。

for i=(1:m);
h = sigmoid(X(i,:)*theta);
J += (-y(i).*(log(h))-(1-y(i)).*(log(1-h)))/m;
end
//----
for i=(1:m);
h = sigmoid(X(i,:)*theta);
grad += ((h - y(i))*X(i,:)')/m;
end

options = optimset('GradObj', 'on', 'MaxIter', 400);

[theta, cost] = ...
	fminunc(@(t)(costFunction(t, X, y)), initial_theta, options);

即可得到训练后的\(\theta\)值，在图上表现出来呈

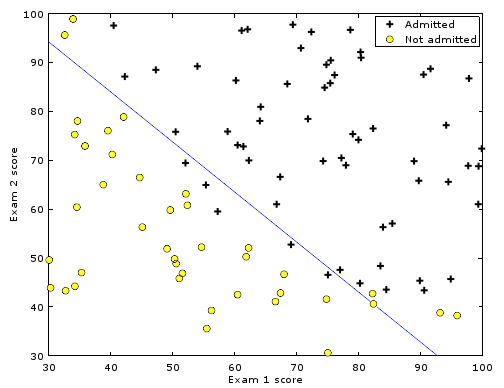
可以看到正集与负集基本分开。

非直线分类

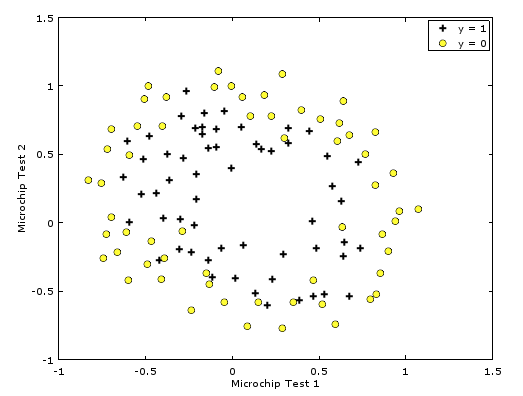
如图所示，可以看出正负集的边界应该是曲线。

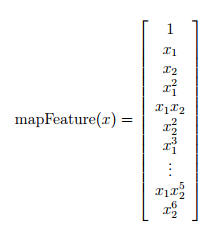
曲线的方程是多项式，因此首先对曲线的多项式的项进行罗列：

degree = 6;
out = ones(size(X1(:,1)));
for i = 1:degree
    for j = 0:i
        out(:, end+1) = (X1.^(i-j)).*(X2.^j);
    end
end

以上生成了一个28项的向量作为这个曲线的项。

\[J(\theta)=\frac{1}{m}[\sum^m_{i=1}-y^{(i)}log{h_\theta(x^{(i)})}-(1-y^{(i)})log{(1-h_\theta(x^{(i)})})]+\frac{\lambda}{2m}\sum^n_{j=1}\theta^2_j\]

根据此公式进行代价函数的运算。

由于上式中最后一项\(\theta\)不需要惩罚\(\theta_0\)，因此从\(\theta_1\)开始相乘。由于matlab的下标号是从1开始的，因此最后一项的θ要从2开始相乘。后面的梯度函数同理

\[\frac{\partial J(\theta)}{\partial \theta_0}=\frac{1}{m}\sum^m_{i=1}(h_\theta(x^{(i)})-y^{(i)})x^{(i)}_j, \text{for j=0}\\ \frac{\partial J(\theta)}{\partial \theta_j}=(\frac{1}{m}\sum^m_{i=1}(h_\theta(x^{(i)})-y^{(i)})x^{(i)}_j)+\frac{\lambda}{m}\theta_j ,\text{for j}\geq 1\]

简单用循环写代码如下

for i=(1:m);
h = sigmoid(X(i,:)*theta);
J += (-y(i).*(log(h))-(1-y(i)).*(log(1-h)))/m;
end
for j=(2:size(theta))
J += theta(j)^2.*lambda/(2*m);
end
//-------
for i=(1:m);
h = sigmoid(X(i,:)*theta);
grad += ((h - y(i))*X(i,:)')./m;
end

for j=(2:size(theta))
grad(j) += theta(j).*lambda./m;
end

可以得到多项式的各个\(\theta\)值。

根据多项式画出图形可以看到

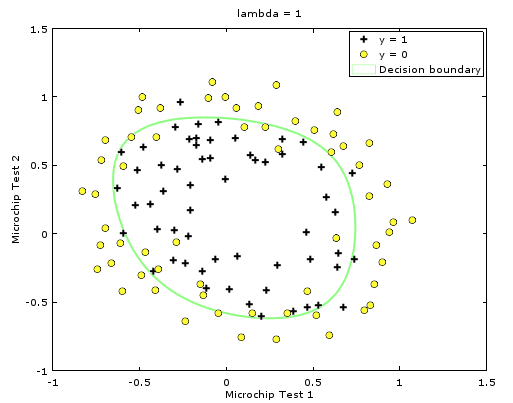
基本将正负极分开。

如果对\(\lambda=1\)(正则化参数)进行修改，例如修改成别的值可以得到：

\(\lambda=0\)

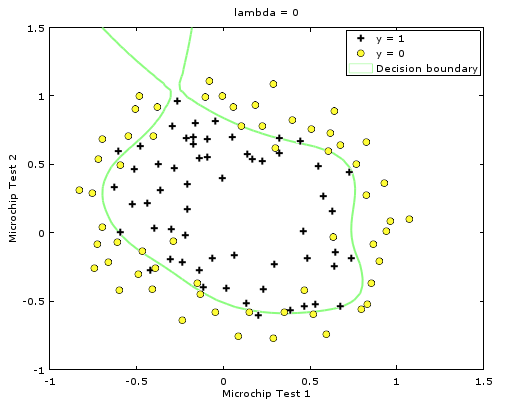
\(\lambda=100\)

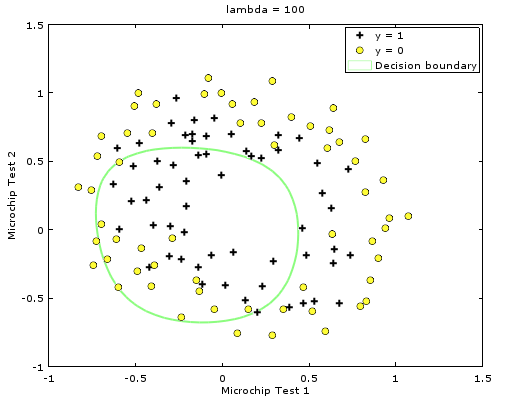
可以看到\(\lambda=0\)的时候拟合曲线绕的弯非常多，试图去匹配所有的点，因而失去了这个集整体的特征，变得过度复杂，这种现象称为过拟合；

而\(\lambda=100\)的时候明显拟合曲线并没有良好地工作，称为欠拟合（\(\theta\)的乘积占的权重过大导致除了θ0之外的项全部变为0）。