机器学习学习笔记(七)分类问题
举例:电子邮件的垃圾邮件判断;在线翻译的正确与否;肿瘤的良性或恶性等。
共性:都是要判断一个集y,
\[y \in \{0,1\}\]
y=0被称为负类,y=1被称为正类。通常上来说负类表示缺少某样东西(例如缺少而行肿瘤)
实际情况多为多类分类(y为3或更多)
实际分类举例:
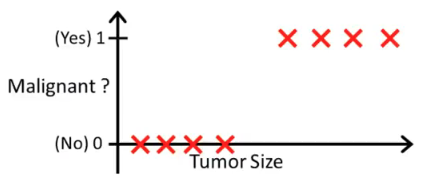
尝试用线性回归拟合这个训练集,发现通常会得到不好的预测结果。
在二元分类中,线性回归预测方法并不适用。因为分类集只有0或1,而线性回归的预测往往会出现小于0与大于1出现。
学习新算法:逻辑回归算法(Logistic Regression):
\[0 \leq h_\theta(x)\leq 1\]
输出值不会小于0,也不会大于1.这个算法是一种分类算法,适用于y标签离散的情况。
\[h_\theta=g(\theta^T x)\]
\[g(z)=\frac{1}{1+e^{-z}}\]
这个函数被称为S型函数。函数图形如下
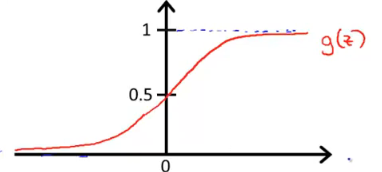
g(z)在z趋近负无穷的时候趋近于0,z趋近正无穷的时候趋近与1.
使用这个假设函数来拟合离散的事件。
由于二元分类问题只有0或1,因此可以与概率问题等同考虑。例如上面病人得肿瘤的例子,当知道他的肿瘤大小后,通过逻辑回归算法得到他得恶性肿瘤的概率为70%那么他得良性肿瘤的概率就是30%。
概念:决策边界(decision boundary)
对于S行函数来说,当输出y=1的概率大于等于0.5时,可以预测输出为1;概率小于0.5时,预测输出为0。
根据图像可以发现z>0是g(z)<0.5。
因此\(\theta^T x\)大于等于0时就能预测输出为1,反之亦然。
决策边界将样品集分为了两个部分,一个部分预测为1一个部分预测为0.
决策边界是假设函数本身的属性,而不是数据集的属性。它包括假设函数的几个参数。
多项式逻辑回归。与单项式相同,只是在式中多加上了多次项。举例:

当$ -1+x2_1+x2_2 $时可以预测y=1
它的决策边界是以原点为圆心,半径为1的圆。因此圆外的一切样本都将被预测为0.