机器学习学习笔记（六）

正规方程

在一些线性回归问题中，可以用正规方程方法更快地解决问题，直接解出参数值来。

设特征矩阵为X（第一列是$x_0=1$）,训练集结果为向量y，能够带入公式

$$\theta = (X^T X)^{-1}X^T y$$

直接解出$\theta$的向量。

举例：

upload successful

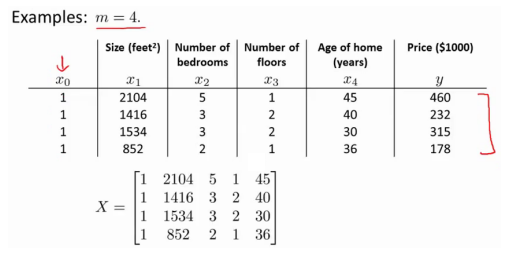
带入公式进行矩阵运算即可得出结果。 以此题为例，我使用 Octave 进行了运算

先输入输入值X的矩阵

upload successful

输入输出值y的向量

upload successful

直接带入公式

$$\theta = (X^T X)^{-1}X^T y$$

upload successful

---

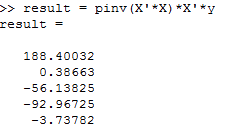
梯度下降法与正规方程的对比

梯度下降	正规方程
需要选择学习率$\alpha$	不需要
需要多次迭代	一次运算得出
当特征数量 n 大时也能较好适用	需要计算$(X^TX)^{-1}$ 如果特征数量 n 较大则运算代价大，因为矩阵逆的计算时间复杂度为 $O(n^3)$，通常来说当 n 小于 10000 时还可以接受
适用于各种类型的模型	只适用于线性模型，不适合逻辑回归模型等其它模型