机器学习学习笔记(五)
特征缩放(Feature Scaling)
在线性回归的实际例子中中多数会遇到这样的情况,某两个特征值的数值相差很远,例如房价可能是100(万元)的数量级,房屋面积可能是100的数量级。表现在轮廓图上的形式就是如下图一样,

等高线(代价函数J)的形状呈现出非常细长的椭圆。
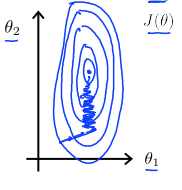
可以看到在这种情况下的梯度下降函数需要迭代很多次,在最小值附近震荡直到最后收敛。为了使梯度下降能够尽量朝着一个方向有效率地进行,我们需要对输入值中的某些特征值进行统一的缩放。
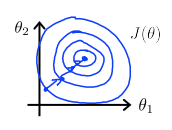
这样的参数值接近的代价方程,梯度下降函数的迭代就会方便与均匀很多,从而达到减少迭代次数的目的。一般来说,将两个参数都缩放到-1,1之间较为合适。特征缩放可直接参照公式:
\[x_n=\frac{x_n-\mu _n}{S_n}\]
其中 \(\mu_n\) 是平均值,\(S_n\) 是标准差。
为了简单方便,可以直接用最大值-最小值来代替标准差。
学习率
学习率α在梯度下降方程中起着重要的作用,梯度下降算法的每次迭代受到学习率的影响,如果学习率 α过小,则达到收敛所需的迭代次数会非常高;如果学习率α 过大,每次迭代可能不会减小代价函数,可能会越过局部最小值导致无法收敛。
在一个线性回归情况中尝试多个学习率可以找到计算效率最高的学习率。通常可以考虑尝试些学习率:α=0.01,0.03,0.1,0.3,1,3,10 (它们都是3倍3倍地增加)
多项式回归
在现实情况中,往往线性回归是不足以很好的契合一个数据集的。
例如
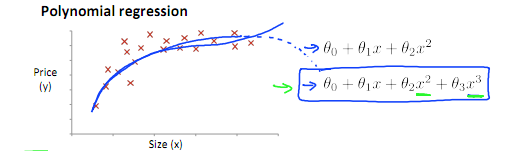
用的三次方程,
其实也可以化为线性方程看:
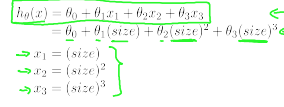
但是经过平方立方之后,每个参数的差值会变得更大,因此特征缩放在这样的情况中更加的重要。
比如上面如果size为1到1000的话,x2就是1到1000000,x3就是1到1000000000。不作处理会使算法很难正常进行下去。可以使x1=size/1000,x2=size2/1000000,x3=size3/1000000000这样就能使几个参数的值在近似的范围内。
再例如
\[h_\theta(x)=\theta_0+\theta_1(size)+\theta_2\sqrt{(size)}\]
要看成
\[h_\theta(x)=\theta_0+\theta_1x_1+\theta_2x_2\]
线性方程,size在1-1000间,那么\(x_1=\frac{size}{1000},x_2=\frac{\sqrt{size}}{\sqrt{1000}}\)